こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(freely rotating chain)
自由連結鎖の問題点
まず、以前紹介した自由連結鎖という最も単純な高分子モデルについて、軽くおさらいをやります。
自由連結鎖は結合長が一定で結合角がランダムという条件でモノマーをつないだモデルです。
平均二乗両末端間距離および回転半径を計算するのが簡単で、とても扱いやすいモデルなのですが、例えば\(\rm{sp}\)\(^3\)炭素なら約\(109.5^\circ\)という結合角をとりやすいなどといったことがまったく考慮されていません。
詳しくはこちらの記事を参照してください。

そのため、実際の高分子を表現するには、より多くの条件が必要になってくる場合が多いです。
自由回転鎖
そこで次に出てくるのが自由回転鎖というモデルです。
これは結合長を\(b\)、結合角を\(\theta\)として、両方のパラメータが一定となることを考えたモデルです。
両方固定しても内部回転角\(\phi\)はランダムな値をとるため、両末端間距離および回転半径が1つの値に定まることはありません。
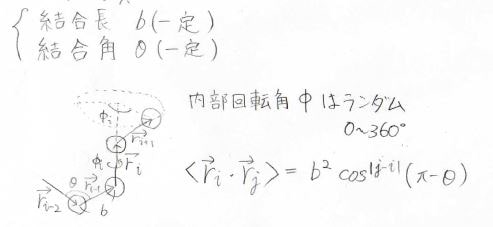
このとき、結合ベクトル\(r_i\)と\(r_j\)の積について、ランダムな内部回転角をとったときの平均をとると\(b^2\cos^{|j-i|}{(\pi-\theta)}\)となります。
したがって、平均二乗両末端間距離は、以下のように計算されます。
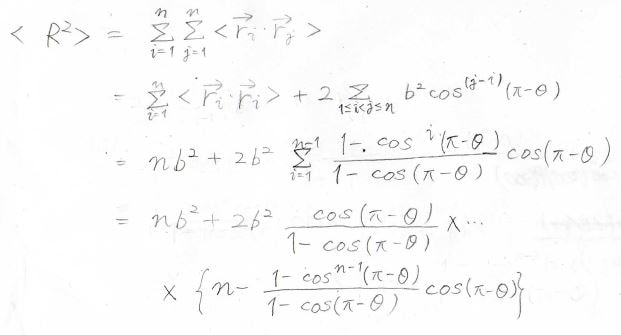
\(i\)と\(j\)が同じ場合と異なる場合で2項に分けて、第一項は自由連結鎖同様に\(nb^2\)となります。
第二項は等比数列の和として計算できます。
そして、結合角\(\theta\)は一般的に\(0\)から\(\pi\)までの間の値をとるため、\(\cos^n(\pi-\theta)\)は\(1\)より十分に小さくなり、無視できると考えることができます。
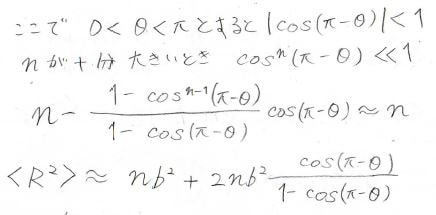
加法定理より、\(\cos{(\pi-\theta)}=-\cos{\theta}\)となるので整理します。
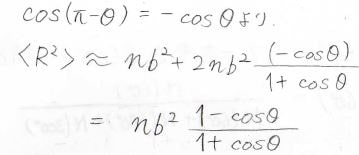
最終的に、自由回転鎖の平均二乗両末端距離は、自由連結鎖の値である\(nb^2\)に\(\displaystyle \frac{1-\cos{\theta}}{1+\cos{\theta}}\)をかけた値になります。
また、この式をモノマー間ベクトル\(\boldsymbol{R}_{ij}\)に当てはめて、Lagrangeの定理より平均二乗回転半径を計算すると、下のようになります。
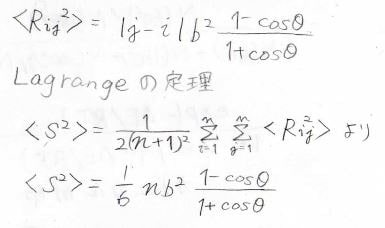
\(\displaystyle \frac{1-\cos{\theta}}{1+\cos{\theta}}\)の部分には\(i\)も\(j\)も入っていないので、自由連結鎖同様に\(\displaystyle \langle S^2\rangle=\frac{1}{6}\langle R^2\rangle\)という関係になります。
束縛回転鎖
自由回転鎖の話はここまでで、もう1つのモデルも紹介したいと思います。
先ほどは結合角を一定にして内部回転角をランダムとしましたが、実際には立体障害の小さな配座をとろうとするはずです。
そこで、それぞれの内部回転角の存在確率が内部回転ポテンシャルによって決まるモデルを考えます。
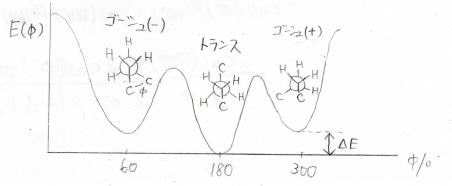
これが束縛回転鎖です。
図はポリエチレンを例にしていますが、この場合は主鎖原子がトランスの配座となるのが最もエネルギーが低く、次に2つのゴーシュの配座が安定になります。
ゴーシュの配座は区別のため、ゴーシュ(+)、ゴーシュ(-)とされることもあります。
平均二乗両末端間距離は先ほどと似た形で、下のようになります。
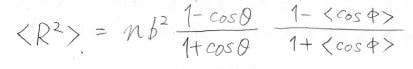
ここで、\(\langle \cos{\phi}\rangle\)は\(\cos{\phi}\)の平均値です。
そしてここからは簡単のため、内部回転角\(\phi\)は\(60^\circ\)、\(180^\circ\)、\(300^\circ\)のみを値としてとることにします。
トランスと2つのゴーシュ以外の配座は考えないこのモデルは、回転異性体近似モデルと言います。
ゴーシュとトランスのエネルギー差を\(\Delta E\)とすると、ボルツマン分布より、下の関係が成り立ちます。
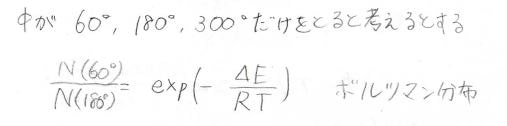
\(\phi\)が\(60^\circ\)になる確率を\(P(\phi)\)とすると、それはカノニカル分布の形で表されます。
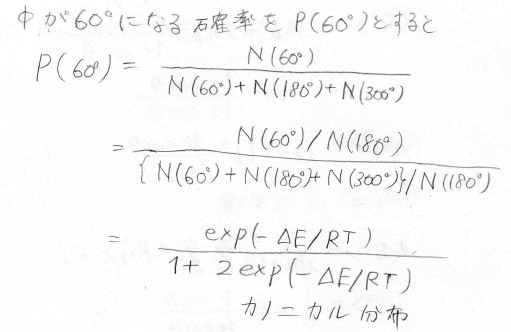
したがって、\(\langle \cos{\phi}\rangle\)は下のように計算されます。
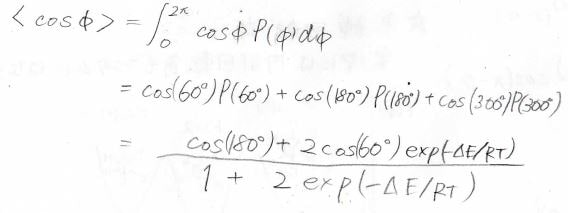

これを平均二乗両末端間距離の式に代入することで、このような関係が得られます。

この式は、\(\Delta E\)を\(0\)にすると、自由回転鎖の式と同じになります。
つまり、トランスと2つのゴーシュを等確率にした場合と、すべての内部回転角を等確率にした場合は同じ結果になるということです。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!



