こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマは、こちら！
動画はこちら↓
動画で使ったシートはこちら(internal pressure)
それでは内容に入っていきます！
内圧の定義と物理的な意味
まずは、前提の話です。
ここでは内部エネルギー\(U\)が体積\(V\)と温度\(T\)の二変数関数であるとします。
理想気体であれば、内部エネルギーは温度だけで決まるため、ここではより一般的な系を考えています。
その全微分はこのように表されまして、第一項の\((\frac{\partial U}{\partial T})_V\)は定積熱容量\(C_V\)となります。
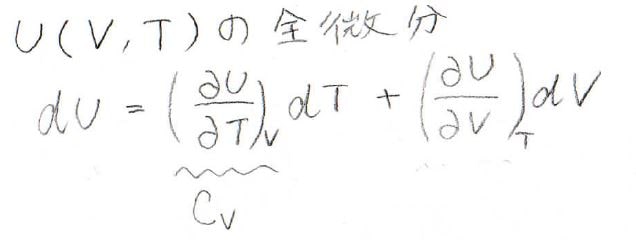
そして、第二項の\((\frac{\partial U}{\partial V})_T\)、これを内圧\(\pi_T\)として定義します。
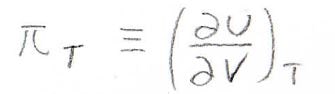
エネルギーを体積で割った単位を持つので、圧力と同じ次元のパラメータとなります。
そして内圧は、分子間相互作用を反映しており、その符号によって、反発力が優勢なのか、引力が優勢なのかがわかります。
温度を一定として、グラフで表したのがこちらです。
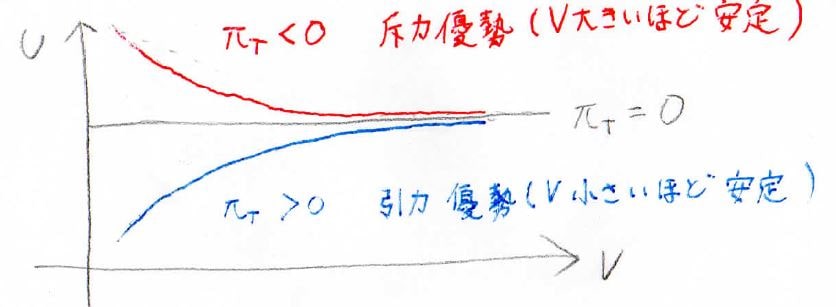
赤い線は内圧が負のとき、つまり体積が大きいほど安定なときに対応しています。
分子間距離は長い方が安定ということなので、これは分子間で反発力が優勢になっていることを意味します。
反対に、青い線は内圧が正のときで、分子間引力が優勢となっています。
内圧が\(0\)のときには、分子間で引力も反発力もはたらいていないということなので、これが理想気体に対応します。
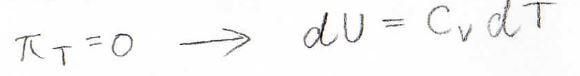
膨張率、等温圧縮率の定義
次に、膨張率と等温圧縮率という量を定義していきます。
まず、膨張率は圧力一定条件で、温度が上昇したときに、体積がどれくらいの割合膨張するのかという量です。
文字\(\alpha\)で表すことにすると、このように定義されます。
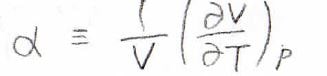
そして等温圧縮率は、温度一定条件下で、圧力を大きくしたときに、体積がどれくらいの割合小さくなるのかという量です。
\(\kappa_T\)と表すことにすると、このように定義されます。
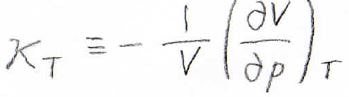
この\(\kappa_T\)は、体積がどれだけ小さくなるかという量ですから、マイナスが付くことに注意してください。
定圧熱容量と定積熱容量の差
それで、\(\rm{d}U\)の式を使って圧力一定条件下における\((\frac{\partial U}{\partial T})_p\)を求めると、このようになります。
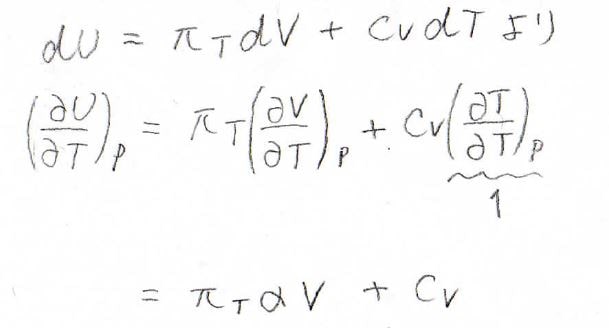
\((\frac{\partial V}{\partial T})_p\)の部分は\(\alpha V\)と書き換えられるため、\((\frac{\partial U}{\partial T})_p=\pi_T \alpha V+C_V\)となります。
この関係式を使うと、定圧熱容量\(C_p\)と定積熱容量\(C_V\)の差を求めることができます。
理想気体
まず理想気体については、内圧\(\pi_T=0\)となるため、\((\frac{\partial U}{\partial T})_p=(\frac{\partial U}{\partial T})_V=C_V\)が成り立ちます。
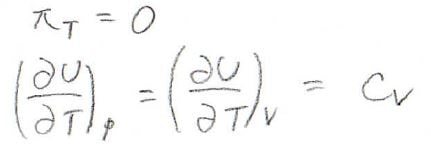
エンタルピーの定義\(H=U+pV\)と、定圧熱容量の定義\(C_p=(\frac{\partial H}{\partial T})_p\)を使うと、\(C_p-C_V=[\frac{\partial (pV)}{\partial T}]_p\)と変形できます。
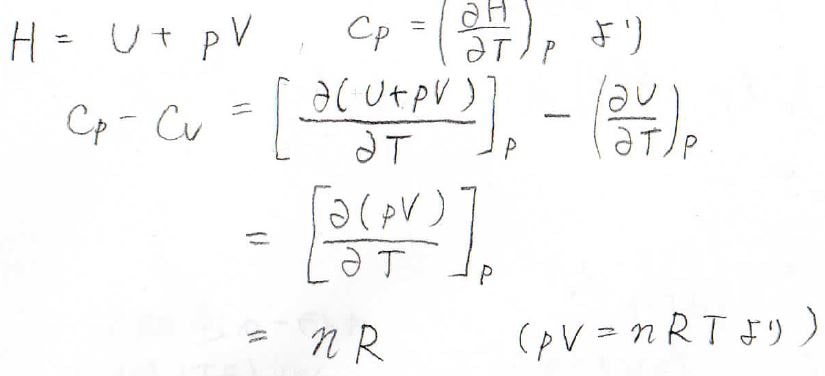
これは理想気体の状態方程式\(pV=nRT\)より\(nR\)となり、マイヤーの式が導かれます。
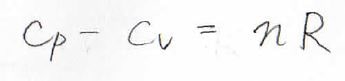
ここで、\(n\)は物質量、\(R\)は気体定数です。
マイヤーの式の導出は、以下の記事でも解説しています。
一般的な系
そして一般的な系では、\((\frac{\partial U}{\partial T})_p\)の式より、\(C_V=(\frac{\partial U}{\partial T})_p−\pi_T(\frac{\partial V}{\partial T})_p\)となるため、ここから\(C_p-C_V\)を求めます。
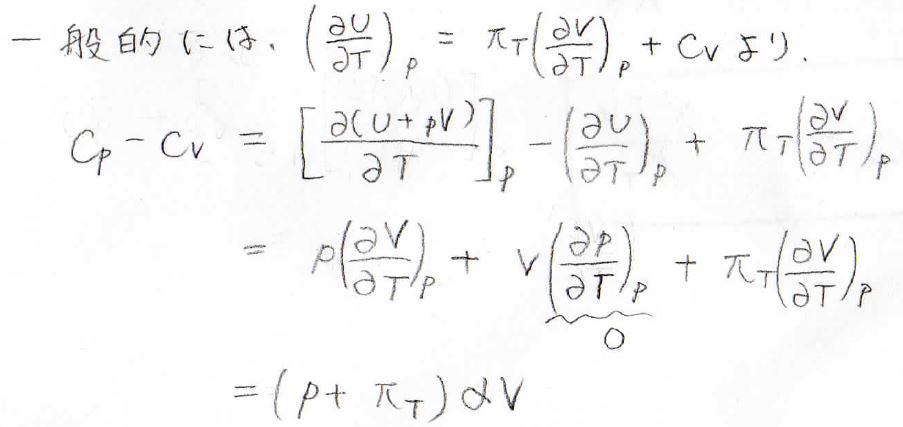
すると、\((\frac{\partial V}{\partial T})_p=\alpha V\)より、\(C_p-C_V=(p+\pi_T)\alpha V\)という関係が導かれます。
この式はさらに変形することができます。
続きは、こちらの記事の練習問題をご覧ください。
熱力学基本式を用いた変形
使うのは、熱力学基本式で、\(S\)はエントロピーを指します。
内圧\(\pi_T=(\frac{\partial U}{\partial V})_T\)でしたが、熱力学基本式より、このように書くことができます。
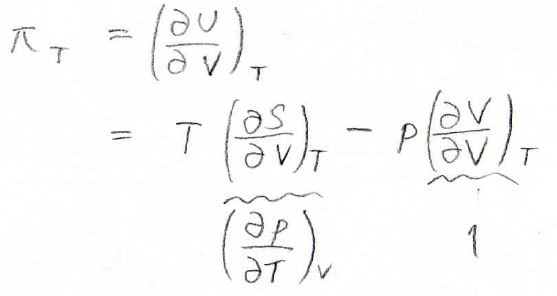
マクスウェルの関係式\((\frac{\partial S}{\partial V})_T=(\frac{\partial p}{\partial T})_V\)より、\(\pi_T=T(\frac{\partial p}{\partial T})_V−p\)となります。
つまり、\(p+\pi_T=T(\frac{\partial p}{\partial T})_V\)という関係が成り立つため、\(C_p-C_V=\alpha TV(\frac{\partial p}{\partial T})_V\)となります。
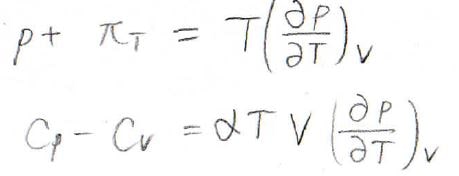
ここで、体積\(V\)を圧力\(p\)と温度\(T\)の二変数関数としてみなすと、その全微分\(\rm{d}V\)は↓のように書けますが、これを利用します。
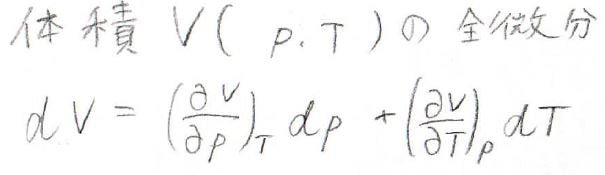
もし体積が一定である場合には、\((\frac{\partial V}{\partial p})_T dp=−(\frac{\partial V}{\partial T})_p dT\)となるため、これを整理すると、\((\frac{\partial p}{\partial T})_V=−\frac{(\frac{\partial V}{\partial p})_T}{(\frac{\partial V}{\partial T})_p}\)となります。
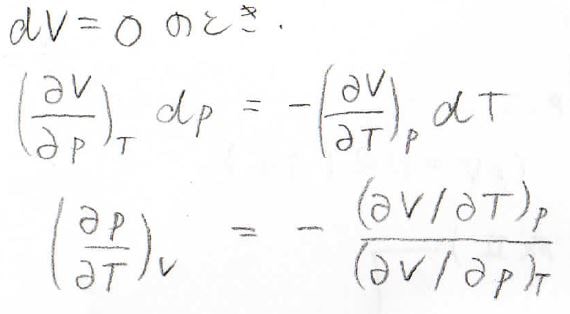
この関係は、オイラーの連鎖式と呼ばれているものです。
そして、\(\frac{(\frac{\partial V}{\partial p})_T}{(\frac{\partial V}{\partial T})_p}=-\frac{\alpha}{\kappa_T}\)となりますから、結局\(C_p-C_V=\frac{\alpha^2 TV}{\kappa_T}\)という関係式が導かれます。
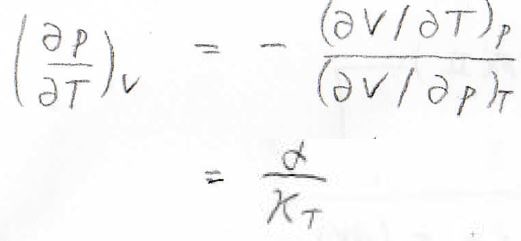
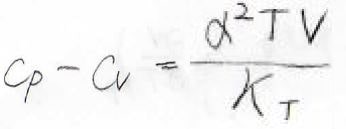
したがって、一般的な系に関して、2つの熱容量の差は膨張率と定温圧縮率を使って表すことができます。
特に、理想気体の場合の場合は、右辺が\(nR\)になりますので、また確かめておいてください。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
