こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓

動画で使ったシートはこちら(polymer geometry)
それでは内容に入っていきます!
高分子の長さパラメータ
溶液中の高分子は空間的な広がりをもち、濃度が高い場合にはそれらが接触し、やがて絡み合いが起こります。
これによって、高分子溶液は濃度によって特性が大きく変わるという特徴があります。
これを議論する場合には、高分子の広がりを表すパラメータが必要になります。
それをどのように表現するのかということが今回の趣旨です。
ここでは、下図のように線状高分子を粗視化して、説明していきます。
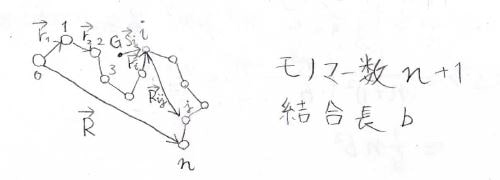
ここで、白い丸はモノマーを表しており、全部で\(n+1\)個あります。
結合長は\(b\)、結合数は\(n\)とします。
ここからは、高分子を評価する3つの長さパラメータについてお話ししていきます。
全長
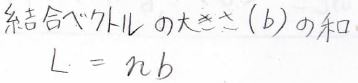
高分子の全長は、結合長と結合数の積として計算できます。
全長が長いほうが広がった分子形態をとりやすいのは確かなのですが、その広がり具合には鎖の剛直性や溶媒との親和性が影響するため、全長だけで分子の広がりを表現することはできません。
そこで、これから紹介する量を定義します。
両末端間距離
両末端を結んだベクトルを両末端間ベクトル\(\boldsymbol{R}\)、その大きさ\(R\)を両末端間距離と呼びます。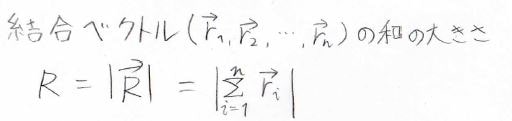
鎖が剛直だった場合は、まっすぐ伸びた形の方がエンタルピーが小さい、つまり安定であるため、全長が同じでも\(R\)は長くなります。
屈曲しやすい場合は、丸まった方がエントロピー的に有利であるため、\(R\)は短くなります。
ただし、溶液中でブラウン運動している高分子鎖の両末端間距離には、ランダムな要素が含まれているため、個々の値を予想することはできません。
二乗の平均をとることでランダムな要素を排除できるため、実際に評価する場合は、平均二乗両末端間距離を使います。
回転半径
そして、もう1つ考え方があります。
それは、高分子の重心\(G\)から各モノマーまでをつないだベクトルを\(\boldsymbol{s}_i\)としてその大きさの平均を回転半径として定義する方法です。
イメージは下図の右下のとおりで、高分子を粒子に見立てたときの半径だと思ってください。

こちらも両末端間距離同様にランダムな要素を含むので、実際の評価には二乗の平均を使います。
なお、重心の定義より、すべての\(\boldsymbol{s}_i\)を足すと\(\boldsymbol{0}\)になります。
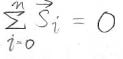
なぜ両末端間距離だけでなく、回転半径を考えるのかということには理由があります。
まず、両末端間距離は末端が2つのときしか定義することができないため、星型高分子、環状高分子などに対応できません。
そして、実験的には回転半径の方が求めやすいからです。
Lagrangeの定理
それではここから平均二乗両末端間距離と平均二乗回転半径の関係を導くときに用いる、Lagrangeの定理というものを導いてみたいと思います。
まずは、下の図をご覧ください。
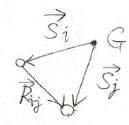
\(i\)番目のモノマーと\(j\)番目のモノマーを結んだベクトルをモノマー間ベクトル\(\boldsymbol{R}_{ij}\)とすると、\(\boldsymbol{R}_{ij}\)は\(\boldsymbol{s}_j-\boldsymbol{s}_i\)で表すことができます。
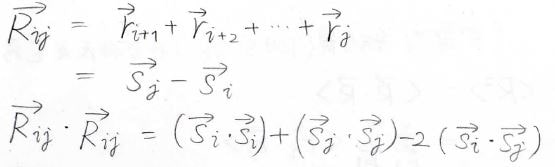
\(\boldsymbol{R}_{ij}\)同士の内積も\(\boldsymbol{s}_i\)と\(\boldsymbol{s}_j\)で表すことができます。
両辺に対して\(i\)と\(j\)の二重和を考えると、以下のようになります。
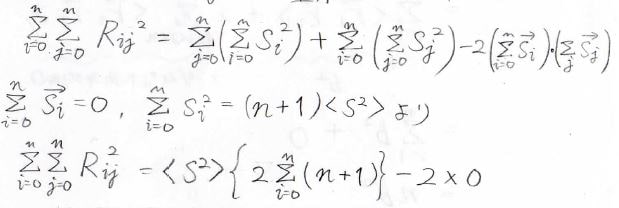
重心の定義、二乗の平均という定義より変形しています。
右辺の\(\displaystyle \sum\)の部分は、\(n+1\)を\(n+1\)回足すという意味なので、\((n+1)^2\)となり、下の関係式が導かれます。
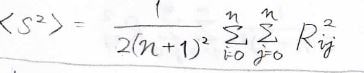
この式のことをLagrangeの定理と呼びます。
この式が意味することとはつまり、重心の位置がどこかわからなかったとしてもモノマー間ベクトルから平均二乗回転半径を求めることができるということです。
これで分岐高分子、環状高分子にも広く対応できるというわけです。
自由連結鎖
それでは最後、単純な高分子モデルに対して実際に式の変形を行い、平均二乗両末端間距離と平均二乗回転半径の関係を導いてみましょう。
今回使う高分子モデルは、自由連結鎖と呼ばれるものです。
これは結合長が\(b\)という一定の値で、結合角はすべての値を等確率で、つまり完全にランダムな値をとるとしたものです。
通常、\(\rm{sp}\)\(^3\)炭素であれば、およそ\(109.5^\circ\)をとりやすいこともあって、結合角がランダムになるとは考えにくいのですが、ここでは考慮しないことにします。
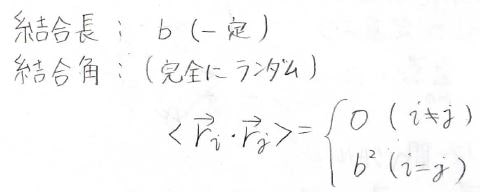
そのとき、\(\boldsymbol{r}_i\)と\(\boldsymbol{r}_j\)の内積は、\(b^2 \times \delta_{ij}\)になります。
ここで、\(\delta_{ij}\)はクロネッカーのデルタです。
すなわち、\(i\)と\(j\)が同じときに\(b^2\)、異なるときには相関がまったくないので、平均をとると\(0\)になります。
平均二乗両末端間距離を求めると、下のようになり、\(nb^2\)と出てきます。

ここで、モノマー間ベクトルをモノマー数が\(|j-i|\)の短い自由連結鎖の平均二乗両末端間ベクトルとしてみると、\(R_{ij}^2=|j-i|b^2\)と書けます。
したがって、Lagrangeの定理から平均二乗回転半径も求めることができます。
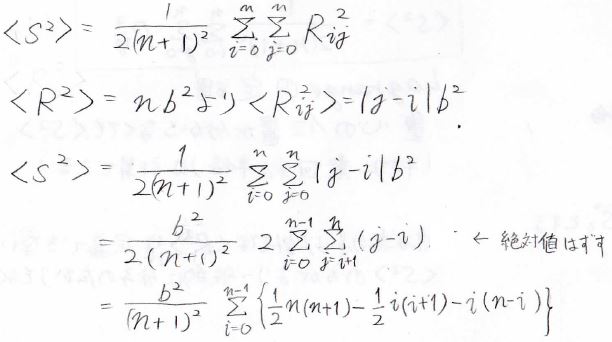

いまは高分子を考えているので、\(n\)がとても大きいという近似を入れると、結局\(\displaystyle \frac{1}{6}nb^2\)と出てきます。
\(nb^2\)は平均二乗両末端間距離だったので、こちらの関係となります。
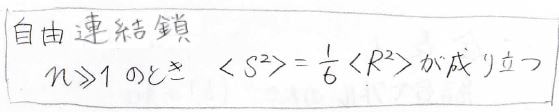
これが自由連結鎖についての両末端間距離と回転半径の関係になります。
ただし、これは必要十分条件ではなく、逆の命題には反例があります。
つまり、平均二乗回転半径が平均二乗両末端間距離の\(\displaystyle \frac{1}{6}\)倍でも、必ずしも自由連結鎖であるとは言えません。
詳しくは、こちらの記事をご覧ください。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!



