こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(relaxation)
それでは内容に入っていきます!
平衡へと向かう反応の速度論
まず、今回考える反応はこちらです。

化学種\(\rm{A}\)、\(1\)分子と化学種\(\rm{B}\)、1分子で化学平衡となっています。
順反応、逆反応ともに\(1\)次反応であるとします。
反応速度定数は、それぞれ\(k\)、\(k’\)です。
反応開始時点である時刻\(0\)では、\(\rm{A}\)だけが存在している状態であったとします。
\(\rm{A}\)のモル濃度の時間変化\(\displaystyle \frac{\rm{d}[\rm{A}]}{\rm{d}\mathit{t}}\)は、\(-k[\rm{A}\)\(]+k'[\rm{B}]\)と書けます。
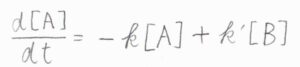
時刻\(0\)での\(\rm{A}\)のモル濃度を\([\rm{A}\)\(]_0\)とすると、\([\rm{A}\)\(]+[\rm{B}\)\(]=[\rm{A}\)\(]_0\)より、\([\rm{B}\)\(]=[\rm{A}\)\(]_0-[\rm{A}]\)と書けます。
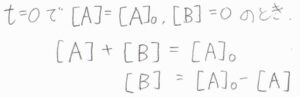
これを代入すると、\(\displaystyle \frac{\rm{d}[\rm{A}]}{\rm{d}\mathit{t}}=-(k+k’)[\rm{A}\)\(]+k'[\rm{A}\)\(]_0\)という微分方程式になります。
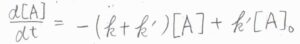
少しテクニカルですが、これは\(\displaystyle \frac{\rm{d}}{\rm{d}\mathit{t}}([\rm{A}]\)\(\displaystyle -\frac{k’}{k+k’}[\rm{A}\)\(]_0)=-(k+k’)([\rm{A}\)\(\displaystyle ]-\frac{k’}{k+k’}[\rm{A}\)\(]_0)\)と書き換えられます。
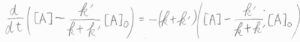
よって、\([\rm{A}\)\(\displaystyle ]-\frac{k’}{k+k’}[\rm{A}\)\(]_0=C\exp{(-(k+k’)t)}\)という一般解が得られます。
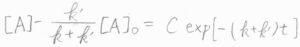
ここで、\(C\)は定数です。
時刻\(0\)で\([\rm{A}\)\(]=[\rm{A}\)\(]_0\)であるため、\(\displaystyle C=\frac{k}{k+k’}\)となります。
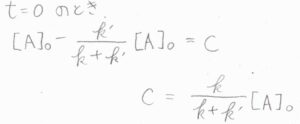
整理すると、\([\rm{A}\)\(\displaystyle ]=\frac{k}{k+k’}[\rm{A}\)\(\displaystyle ]_0\exp{[-(k+k’)t]}+\frac{k’}{k+k’}[\rm{A}\)\(]_0\)という式が得られるため、\(\rm{A}\)のモル濃度は時間の指数関数として減衰することになります。
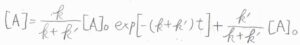
\(\rm{B}\)のモル濃度は、\([\rm{A}\)\(]_0-[\rm{A}]\)より、\(\displaystyle -\frac{k}{k+k’}[\rm{A}\)\(\displaystyle ]_0\exp{[-(k+k’)t]}+\frac{k}{k+k’}[\rm{A}\)\(]_0\)となります。
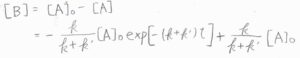
横軸を時刻\(t\)、縦軸を\(\rm{A}\)と\(\rm{B}\)のモル濃度を\([\rm{A}\)\(]_0\)で割った値としてグラフを書くと、下のようになります。
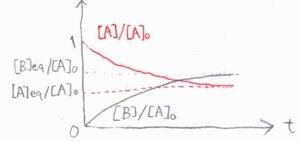
赤が\(\rm{A}\)、黒が\(\rm{B}\)のモル濃度を表しています。
長時間経過すると、いずれも一定の値に収束し、見かけ上は反応が進行しないようになります。
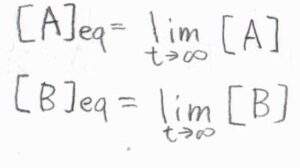
平衡定数\(K\)は、それら長時間極限の比として書けて、\(\displaystyle \frac{k}{k’}\)となります。
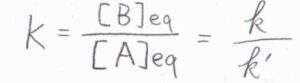
標準反応ギブズエネルギー\(\Delta_\rm{r}\)\(G^\circ\)も\(\displaystyle RT\ln{(\frac{k’}{k})}\)と書けます。
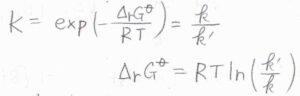
ただし、ここには注意が必要で、平衡定数や標準反応ギブズエネルギーは熱力学的な量であるのに対して、反応速度定数は速度論的な量です。
熱力学的な量は、変化前後の状態量がわかれば、それだけで決まる値で、どのようにしてその変化が起こったのかということはまったく関係ありません。
一方で、速度論的な量は変化の過程を反映した量になります。
例えば、触媒を使ったときと使わなかったときで、反応速度には大きな差が生じますが、それによって平衡定数が変化することはありません。
いま、熱力学的な量と速度論的な量を等式で関係づけられたのは、変化の経路が順反応、逆反応ともに\(1\)次反応であり、他に変化の経路がないことを仮定しているからです。
前提条件なく、これらを等式で関係づけることはできないので、注意してください。
緩和法
さて、後半部分では、緩和法の話をします。
緩和というのは、平衡状態にある系が外界からの影響により非平衡状態となったときに、新たな平衡状態へと向かっていく変化の過程のことを言います。
温度を上げれば、吸熱反応が優勢となるなどといったルシャトリエの原理を利用して、反応速度定数を求めるのが緩和法です。
ルシャトリエの原理については、こちらを参照してください。

ここでは、外界から温度を変化させることを考えるので、反応エンタルピーが\(0\)ではないという仮定のもと、お話ししていきます。
まず、温度\(T_1\)で平衡状態にある\(\rm{A}\)と\(\rm{B}\)があったとします。
そこから時刻\(0\)で温度を\(T_2\)へ変化させます。
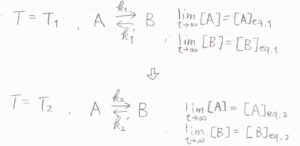
それぞれの温度で、反応速度定数とモル濃度の長時間極限は、上記の添え字を付けて表すことにします。
温度を変化させたちょうどの時刻\(0\)では、それぞれのモル濃度は、温度\(T_1\)での平衡状態の値で書けます。
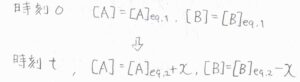
そこから\(t\)だけ時間が経過したときの\(\rm{A}\)と\(\rm{B}\)のモル濃度をそれぞれ\([\rm{A}\)\(]_\rm{eq,2}\)\(+x\)、\([\rm{B}\)\(]_\rm{eq,2}\)\(-x\)と表すことにします。
すると、\(\displaystyle \frac{\rm{d}[A]}{\rm{d}\mathit{t}}=\frac{\rm{d}\mathit{x}}{\rm{d}\mathit{t}}\)であるため、このような微分方程式が得られます。
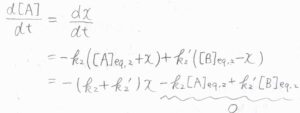
\(-k_2[\rm{A}\)\(]_\rm{eq,2}\)\(+k’_2[\rm{B}\)\(]_\rm{eq,2}\)の部分は反応速度のつり合いより、\(0\)となります。
したがって、\(x=x_0\exp{[-(k_2+k’_2)t]}\)となります。
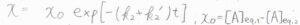
\(x_0\)は、時刻\(0\)での\(x\)であり、\([A]_\rm{eq,1}\)\(-[A]_\rm{eq,2}\)です。
\(\displaystyle \frac{1}{k_2+k’_2}\)は緩和にかかる時間の目安であり、これを\(\tau\)とすると、\(\displaystyle x=x_0\exp{(-\frac{t}{\tau})}\)となります。
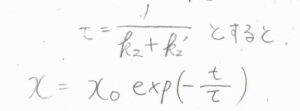
横軸を\(t\)、縦軸を\(x\)とすると、下図左のようなグラフが書けます。

\(\tau\)は、\(x\)が\(\displaystyle \frac{1}{\rm{e}}\)倍まで減衰するのにかかる時間です。
この\(\tau\)と平衡定数\(K\)を実験的に求められれば、\(\displaystyle K=\frac{k_2}{k’_2}\)、\(\displaystyle \tau=\frac{1}{k_2+k’_2}\)より、\(k_2\)と\(k’_2\)をそれぞれ求められることになります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




