こんにちは！
それでは今回も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(tunneling effect)
それでは内容に入っていきます！
言葉で表現すると…
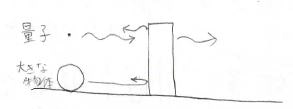
まずトンネル効果を言葉で説明すると、量子はある確率でポテンシャルの障壁を透過する、ということです。
壁に大きな物体をぶつけても跳ね返るだけですが、量子の場合は跳ね返るのは一部で、残りは壁を透過します。
調和振動子に見るトンネル効果
ではここから数式も使ってお話ししていきます。
まずは調和振動子の例です。
まず、マクロに見た場合は物体が振幅\(A\)の単振動をします。
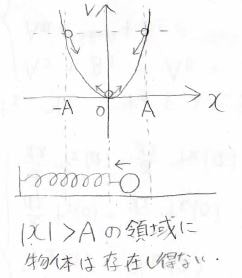
この時\(-A\)より小さい領域、\(A\)より大きい領域に物体は存在しません。
これに対してミクロに見た世界ではエネルギーが不連続となり、波動関数はエルミート多項式\(H_n(\xi)\)と\(\exp{(-x^2)}\)に比例します。
詳しくは過去にあげた調和振動子の記事を参照してください。
そして、量子数が\(0\)の時にはエルミート多項式が\(1\)になって、\(\exp{(-\frac{\alpha^2 x^2}{2})}\times\)規格化定数が波動関数になります。
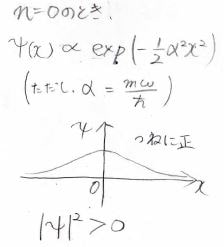
ここで\(\alpha=\frac{m\omega}{\hbar}\)です。
この関数をグラフにすると、上のように常に正となるものになります。
これはすなわち、ポテンシャルカーブの外側の点においても存在確率が\(0\)にならないということになります。
古典的に存在しえない領域に量子がにじみ出るということです。
境界条件から透過比を導出
ではここからはちょっとややこしいですが、入射波のうちどれだけがポテンシャル障壁で跳ね返り、どれだけが透過するのかというのを式で導いてみます。
計算モデル
計算に使うモデルはこの通りです。
\(x\)が\(0\)から\(a\)の領域に大きさ\(V_0\)の壁があって、\(x\)のマイナス側から量子を入射させます。
そして、屈折率が変わる界面では一部の波が跳ね返ります。
このように領域\(\rm{I}\)、\(\rm{II}\)、\(\rm{III}\)と分けると、領域\(\rm{III}\)にある波が透過波ということになります。
各領域の波動関数
それでは次に各領域について波動関数を考えます。
領域Iではポテンシャルが\(0\)なのでシュレディンガー方程式はこのようになり、微分方程式を解いて、\(k_\rm{I}\)を\(\frac{\sqrt{2mE}}{\hbar}\)と置くと、波動関数はこうなります。
ここで、\(\exp{(ik_\rm{I}x)}\)は正方向、\(\exp{(-ik_\rm{I}x)}\)は負の方向へ進む波になります。
これはつまり前者が入射波、後者が反射波になります。
領域\(\rm{II}\)においてはポテンシャルが\(V_0\)であり、\(k_{\rm{II}}\)を\(\frac{\sqrt{2m(V_0-E)}}{\hbar}\)と置くと、さっきと同様に入射波と反射波で書けます。
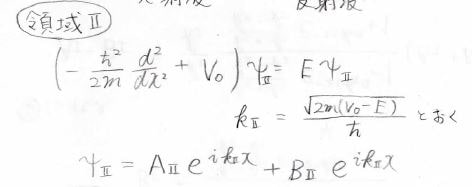
領域\(\rm{III}\)の場合は反射波はなく、また領域と同じくポテンシャルが\(0\)なので、\(k_{\rm{III}}\)は\(k_\rm{I}\)と同じになり、波動関数はこのようになります。
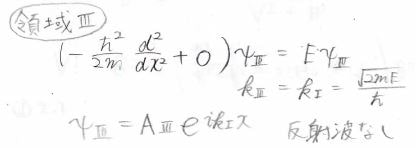
境界条件と透過比
そして次に境界条件を考えます。
2つの領域の境界では、波が不連続になったり、こんな風にカクっと折れることはなくて、滑らかにつながるはずです。
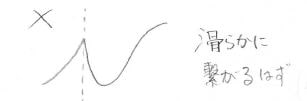
そのため、この4つの式が成り立つことになります。
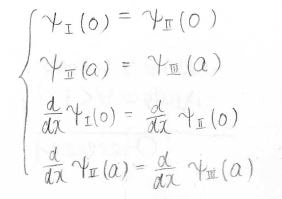
先ほど考えた各領域の波動関数を入れると、こうなります。
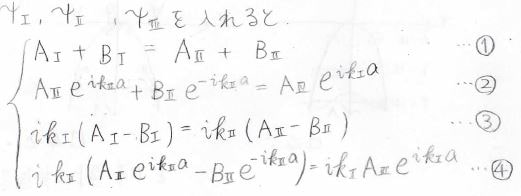
ここで、上から順に①~④式と呼ぶことにします。
求めたいのは反射比と透過比なわけですが、それは波動関数の係数部分の比の2乗で表すことができるので、これを目指して式変形をしていきます。
まずは②式と④式から\(\exp{(ik_\rm{I}a)}\)を消去すると、このように\(A_{\rm{II}}\)を\(B_{\rm{II}}\)で表せます。
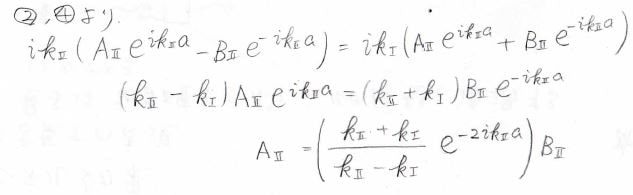
そして①式にこれを代入すると、\(B_{\rm{II}}\)も\(A_\rm{I}\)と\(B_\rm{I}\)で表すことができます。
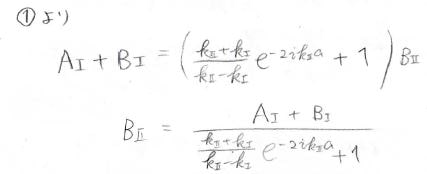
これを③式に代入すると\(A_\rm{I}\)と\(B_\rm{I}\)の比を導くことができ、これの2乗を取るとそれが反射される割合になります。
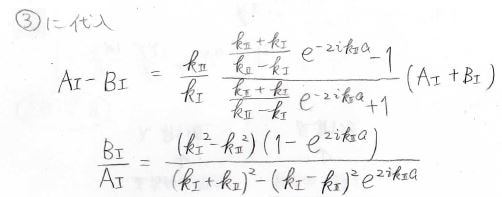
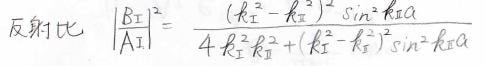
入射した波は反射するか透過するしかないため、\(1\)からこの反射比を引いたものが透過比になり、実際にこのように求めることができます。
この透過比はポテンシャル\(V_0\)の大きさと壁の厚さ\(a\)に依存することになります。
まとめ
はい、それでは今回の内容は以上ですので、最後おさらいをやって終わります。
今回は量子力学のトンネル効果についてお話しました。
トンネル効果は一言でいうと、古典的には存在し得ない領域に量子が滲み出るという現象です。
調和振動子の例では、ポテンシャルカーブの外側の点においても波動関数が\(0\)にならないことから、トンネル効果を説明しました。
最後に紹介した計算モデルでは境界条件を使って透過する波の割合を求めました。
イメージでは当たり前ですが、その割合はポテンシャル障壁の高さ\(V_0\)と厚さ\(a\)に依存するものとして導くことができました。
今回は以上です。
どうもありがとうございました！
