こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(uncertainty principle)
言葉で表現すると?
まず、不確定性原理とは何かを簡単にお話しします。
不確定性とは、はっきりしないということです。
量子の位置と運動量は同時に決めることができず、なんとなくでしか位置を決められないというのが不確定性の簡単な表現です。
ディラックのデルタ関数
ここからは、数式も使っていきます。
今回考える波動関数は、いくつかの単純な波の線形結合とします。
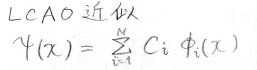
ここで、\(\displaystyle C_i\)は寄与の大きさを表す定数です。
量子の存在確率密度は絶対値の大きさの2乗で与えられます。
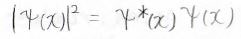
個々の波である\(\phi_i\)は、こちらのように書けるものとします。
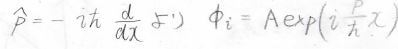
ここで、\(\displaystyle p\)は運動量、\(\displaystyle \hbar\)はディラック定数、\(\displaystyle A\)は規格化定数です。
ここで、仮に量子の位置が\(x_0\)に定まったことを考えましょう。

このとき、存在確率密度は上のグラフのとおりで、式で書くと下のようになります。
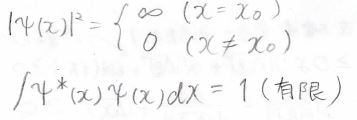
\(x=x_0\)で無限大に発散し、それ以外の点では\(|\psi|^2=0\)になります。
しかし、規格化条件があるため、全範囲で積分すると\(1\)という有限の値になります。
このような関数は数学や自然科学でたびたび見られ、ディラックのデルタ関数と呼ばれます。

\(\delta(0)=\infty\)となるように平行移動させると、右辺は\(\delta(x-x_0)\)となります。
フーリエ級数
実は、偶関数であるデルタ関数は、波長の異なる余弦波の足し合わせとして、表現できます。
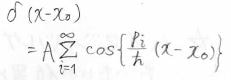
このように、ある関数を\(\sin\)と\(\cos\)の級数で表す操作は、フーリエ展開と言います。
例えば、振幅が同じで、波長の異なる2つの波の和を考えてみましょう。
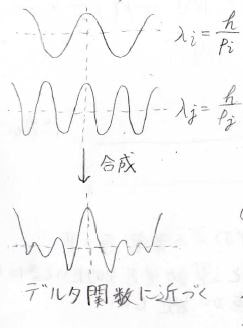
異なる波長の2つの波の和は、\(x=x_0\)の周辺および\(\lambda_i\)と\(\lambda_j\)の公倍数となる点周辺で強め合いますが、それ以外の部分では打ち消しあいが起こり、振幅が小さくなります。
波長の異なる波を無限回足し合わせると、すべての波長の公倍数は無限大となり、\(\displaystyle x=x_0\)でのみ強め合いが起こり、それ以外の点の振幅は\(\displaystyle 0\)に収束します。
そうやって、デルタ関数を作ることができます。
このとき、すべての波の振幅は同じであることが重要です。
あらゆる運動量の波が同じだけ寄与しているということは、量子の位置を厳密に定めた場合に、運動量はあらゆる値をとりうるため、厳密に求まらないことを意味します。
フーリエ変換
運動量を連続量として考えた場合には、フーリエ変換として表現されます。

フーリエ変換は、その関数をフーリエ展開したとき、それぞれの三角関数の寄与の大きさを求められる数学的な操作です。
デルタ関数をフーリエ変換すると、波長に依存しない定数となるため、すべての波長の波の寄与が等しいことがわかります。
\(\Delta\)をその値のブレの大きさとすると、このような表現になります。
![]()
また、運動量を厳密に決めたときにも同様のことが言えます。
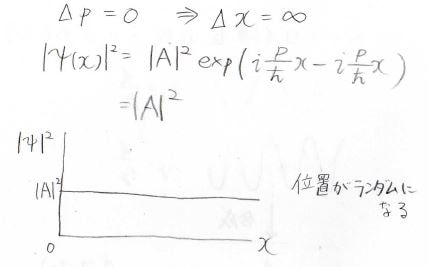
運動量が1つということは、\(\psi\)が1つの波長の波で書けるということですが、そうすると存在確率密度\(|\psi|^2\)は\(x\)に依存しない定数になるため、その量子の位置はランダムになります。
ハイゼンベルグの不確定性原理
最後に、ハイゼンベルグの不確定性原理についてお話しして終わります。
位置と運動量を同時に厳密に定めることはできないので、両方のだいたいの値を最も高い精度で求めたときのことを考えましょう。
最も精度が高いと言えるのは、\(\Delta x\)と\(\Delta p\)の積が最小値をとるときです。
まず、交換子というものを定義します。
2つの演算子\(\hat{\Omega_1}\)、\(\hat{\Omega_2}\)について、それらの交換子\([\hat{\Omega_1},\hat{\Omega_2}]\)をこのように導入します。
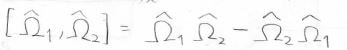
第一項は\(\hat{\Omega_2}\)を先に適用して得られたものに\(\hat{\Omega_1}\)を適用するもので、第二項はその逆の順番で演算子を適用したものになります。
そして、\([\hat{\Omega_1},\hat{\Omega_2}]=\hat{0}\)となったとき、つまり演算子の順番に関係なく導かれる値が等しくなるとき、「\(\hat{\Omega_1}と\hat{\Omega_2}\)は可変である」と言います。
位置を導く演算子\(\hat{x}\)と運動量の\(x\)成分を導く演算子\(\hat{p_x}\)で交換子を考えると、下のようになります。
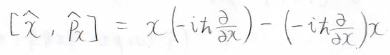
さらに、第二項は下のように変形されます。
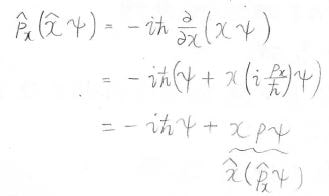
その第二項は、交換子の第一項と一致します。
したがって、\([\hat{x}, \hat{p_x}]=\rm{i}\)\(\hbar\)となり、\(\hat{0}\)ではないので\(\hat{x}と\hat{p_x}\)は可変ではないことになります。

ここで、値のブレの大きさ\(\Delta x\)と\(\Delta p_x\)を演算子として、このように導入します。
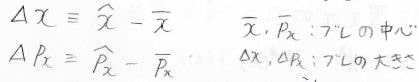
ここで、\(\bar{x}\)、\(\bar{p_x}\)はそれぞれのブレの中心の値です。
そして、不確定性を考慮した波動関数\(\Psi\)をこのように表すことにします。

ここで\(\alpha\)は定数です。
複素数平面において、複素数同士の掛け算はベクトルの回転とみなすことができるため、これにより真の値から少しずれる効果を考えています。
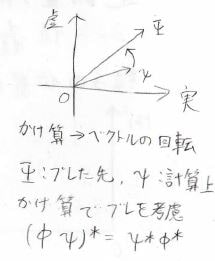
不確定性を加味した場合の存在確率密度\(\Psi^\ast \Psi\)は、下のようになります。

途中、\([\hat{x}, \hat{p_x}]\)が出てくるので、ここに\(i\hbar\)を代入します。
そして、\(\psi^\ast \psi\)は不確定性を考慮する前の存在確率密度であり、\(\Psi^\ast \Psi\)と\(\psi^\ast \psi\)は、どちらも\(0\)以上の値となります。
したがって、\((\Delta x)^2+\alpha^2(\Delta p_x)^2-\alpha\hbar\)も\(0\)以上となります。
ここで簡単のため、これまで演算子で考えていた\(\Delta x\)と\(\Delta p_x\)をそれらによって導かれるスカラー量\(\bar{\Delta x}\)、\(\bar{\Delta p_x}\)と置き換えます。
最小値が\(0\)以上になればよいため、最小値を求めるためにこの式を平方完成すると、下のようになります。
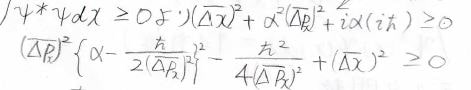
そして、その最小値はこのようになります。

これを整理すると、\((\bar{\Delta x})^2(\bar{\Delta p_x})^2\)の満たすべき条件式が得られます。
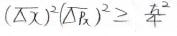
ここで、\(\bar{\Delta x}\)と\(\bar{\Delta p_x}\)をスカラー量のまま\(\Delta x\)、\(\Delta p_x\)と再定義すると、最終的に\(\displaystyle \Delta x\cdot \Delta p_x\geq \frac{\hbar}{2}\)となります。
これが\(\Delta x\)と\(\Delta p_x\)の満たすべき条件で、量子の位置と運動量をこれ以上に精度よく決めることはできません
これをハイゼンベルグの不確定性原理と言います。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!