こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(vibrational spectrum)
振動エネルギー準位
二原子分子\(\rm{A}\)\(-\rm{B}\)の化学結合をばねに見立てたとき、シュレディンガー方程式は下のように書けます。
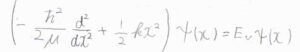
ここで、\(x\)は平行核間距離\(R_\rm{e}\)からの変位、\(\mu\)は換算質量、\(k\)はばね定数です。
そのエネルギーは、\(v\)を\(0\)以上の整数として、\(\displaystyle (v+\frac{1}{2})\hbar \omega\)で与えられます。

\(v\)は振動量子数と言います。
また、\(\displaystyle \omega=\sqrt{\frac{k}{\mu}}\)です。
準位間のエネルギー差は\(\hbar\omega\)で一定となり、多くの化学結合について、このエネルギーに相当する電磁波の波長は、赤外線の範囲に収まります。
詳しくは、こちらを参照してください。

選択律
選択概律
赤外線の吸収、放出を伴って振動状態の遷移が起こるとき、その選択概律は、振動により永久双極子モーメントに変化が生じなければならないことになります。
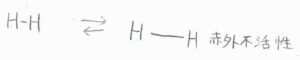
二原子分子の場合、永久双極子モーメントをもつ異核二原子分子は、結合の伸縮により永久双極子モーメントの大きさが変化します。
しかし、等核二原子分子は、たとえ結合距離が変わっても永久双極子モーメントをもつことはないので、赤外不活性となります。

個別選択律
そして、振動遷移の個別選択律は、振動量子数の変化\(\Delta v\)が\(+1\)もしくは\(-1\)となる遷移だけが許容されるというものです。
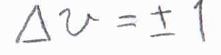
電子状態と回転状態はそのままで、振動遷移だけが起こるとき、状態\(\rm{i}\)から\(\rm{f}\)への遷移双極子モーメント\(\boldsymbol{\mu}_\rm{fi}\)は\(\displaystyle \int \psi_{v_\rm{f}}\)\(^\ast \hat{\boldsymbol{\mu}} \psi_{v_\rm{i}}\)\( \rm{d}\)\(x\)と書けます。
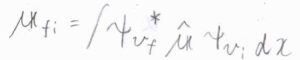
ここで、電気双極子モーメント演算子に、結合距離変化に伴う変化を考慮します。
\(\hat{\boldsymbol{\mu}}_0\)を\(x=0\)のときの電気双極子モーメント演算子として、べき級数でその変化を考えます。
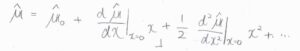
\(x\)は十分に小さいとして第二項以降を無視すると、\(\boldsymbol{\mu}_\rm{fi}\)はこのように書けます。
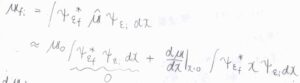
ここで、第一項はエルミート多項式の直交性より\(0\)となるので、第二項が\(0\)ではない値をもつかどうかで、許容遷移か禁制遷移かが判断できます。
伸縮により永久双極子モーメントが変化しない場合には、\(\displaystyle (\frac{\rm{d}\hat{\boldsymbol{\mu}}}{\rm{d}\mathit{x}})_{x=0}=0\)となるので、赤外不活性です。
これが選択概律です。
ここからは、エルミート多項式の性質から個別選択律を導きます。
こちらの記事を参照してください。

エルミート多項式を\(H_v\)、\(\xi=\alpha x\)とすると、\(\displaystyle \xi H_v=v H_{v-1}+\frac{1}{2}H_{v+1}\)という漸化式が成り立ちます。
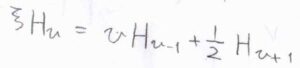
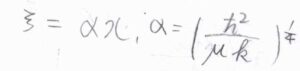
ここで、\(\displaystyle \alpha=(\frac{\hbar^2}{\mu k})^{1/4}\)です。
変数を\(x\)から\(\xi\)に変換すると、遷移双極子モーメント\(\boldsymbol{\mu}_\rm{fi}\)はこちらのように書けます。
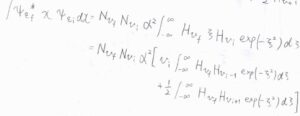
エルミート多項式の直交性より、\(v_\rm{f}\)\(=v_\rm{i}\)\(-1\)のときには、第一項が\(0\)ではない値をもちます。
同様に、\(v_\rm{f}\)\(=v_\rm{i}\)\(+1\)のときには、第二項が\(0\)ではない値をもちます。
\(v_\rm{f}\)がそれ以外の値であるときには、第一項、第二項ともに\(0\)となるため、その遷移は禁制となります。
したがって、振動量子数の変化量\(\Delta v=\pm 1\)、これが振動遷移の個別選択律となります。
ここで、振動エネルギー\(E_v\)を波数単位としたものを\(\tilde{G}(v)\)とします。
\(\displaystyle \tilde{G}(v)=(v+\frac{1}{2})\frac{\omega}{2\pi c}\)であり、\(v\)から\(v+1\)へ遷移したときの吸収波数は、\(\displaystyle \tilde{G}(v+1)-\tilde{G}(v)=\frac{\omega}{2\pi c}\)となります。
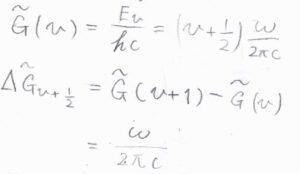
これを\(\displaystyle \Delta \tilde{G}_{v+\frac{1}{2}}\)と表すことにします。
この値は、振動量子数\(v\)には依存しないため、どの振動遷移についても同じ波数で吸収が起こることになります。
非調和性
ただ実際には、吸収波数が\(v\)によって少し変化して、複数のスペクトル線が得られることがあります。
これまでは、化学結合を調和振動子としていましたが、\(v\)が大きい領域では、ポテンシャルエネルギーの放物線近似が成り立たなくなります。
ここでは、化学結合の非調和性を考えるモデルとして、モースポテンシャルを用いて補正することを考えてみます。
モースポテンシャルの式は、\(V=hc\tilde{D}_\rm{e}\)\([1-\exp{(-ax)}]^2\)です。

ここで、\(\tilde{D}_\rm{e}\)はポテンシャルの深さを表す値で、\(\displaystyle a=\sqrt{\frac{\mu \omega^2}{2hc\tilde{D}_\rm{e}}}\)です。
モースポテンシャルをシュレディンガー方程式に入れて計算すると、\(\displaystyle \tilde{G}(v)=(v+\frac{1}{2})\tilde{\nu}-(v+\frac{1}{2})^2x_\rm{e}\)\(\tilde{\nu}\)となります。

ここで、\(\displaystyle \tilde{\nu}=\frac{\omega}{2\pi c}\)、\(x_\rm{e}\)は非調和定数と呼ばれるもので、\(\displaystyle \frac{\tilde{\nu}}{4\tilde{D}_\rm{e}}\)で与えられます。
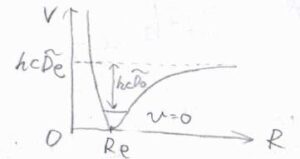
エネルギー準位の間隔は、\(v\)が大きくなるほど小さくなり、エネルギーは\(hc\tilde{D}_\rm{e}\)に収束していきます。
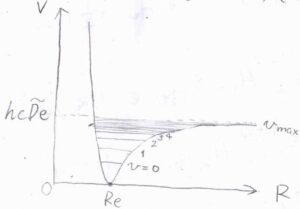
そして、\(v\)のとりうる値の数は有限になり、それ以降はポテンシャルが減少していくことになります。
実用上はより一般的な形として、三次以上の項も考えることで、実験結果に合わせることができます。
![]()
このときの吸収波数\(\displaystyle \Delta \tilde{G}_{v+\frac{1}{2}}\)は、\(\tilde{\nu}-2(v+1)x_\rm{e}\)\(\displaystyle \tilde{\nu}+(3v^2+6v+\frac{13}{4})y_\rm{e}\)\(\tilde{\nu}-\cdots\)となります。
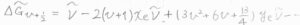
式の中に\(v\)が入っているため、どこの準位間で遷移が起こったかによって、吸収波数が変化しうる形になっています。
また、前半で考えた振動遷移の個別選択律ですが、これは調和振動子を仮定したものであり、非調和性が存在するときには、\(|\Delta v| \gt 1\)の遷移も低確率ながら許容されることになります。
実際に、\(\Delta v=1\)の吸収波数の整数倍に近いところに弱い吸収線が観測されることがあり、\(|\Delta v|=2\)の遷移は第1の倍音、\(|\Delta v|=3\)の遷移は第2の倍音と言います。
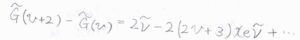
ビルゲースポーナーのプロット
最後に、モースポテンシャルにおいて、基底状態のポテンシャルの深さを見積もる方法として、ビルゲースポーナーのプロットを紹介して終わります。
\(\tilde{D}_0=\tilde{D}_\rm{e}\)\(-\tilde{G}(0)\)とすると、これは\(\displaystyle \sum_{v=0}^{v_\rm{max}}\)\(\displaystyle \Delta \tilde{G}_{v+\frac{1}{2}}\)と書けます。
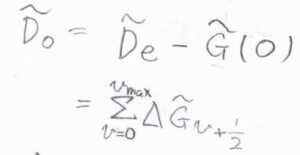
すなわち、横軸に\(\displaystyle v+\frac{1}{2}\)、縦軸に吸収波数\(\displaystyle \Delta \tilde{G}_{v+\frac{1}{2}}\)をとったグラフを書くと、下図の斜線部の面積から、基底状態のポテンシャルの深さを見積もることができます。
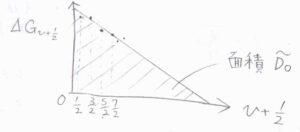
このグラフは、非調和定数\(\displaystyle x_\rm{e}\)だけを考慮したモースポテンシャルで、\(\displaystyle v+\frac{1}{2}\)は傾きが負の一次関数となります。
強度が弱い吸収は直線補外することで、三角形の面積が求められます。
ただし実際には、\(v\)が大きく非調和性が大きく現れる領域では、グラフが直線から外れてしまうため、この方法では、\(\tilde{D}_0\)は真の値よりも常に過大評価されることになります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




