こんにちは!
それでは今日も化学のお話やっていきます。
動画はこちら↓
動画で使ったシートはこちら(x-ray diffraction)
X線発生装置
まず、X線を発生させる装置の原理について、少しだけお話しします。
X線とは、波長が\(1\ \rm{pm}\)から\(10\ \rm{nm}\)程度ととてもエネルギーの大きな電磁波のことです。
単位胞の辺の長さや格子面の間隔は、可視光の波長よりもとても短いため、光学顕微鏡で拡大しても観察することができません。
そこで、結晶構造の解析には、ずっと波長の短いX線が使われます。
こちらの図は、X線を発生させる装置を表したものです。
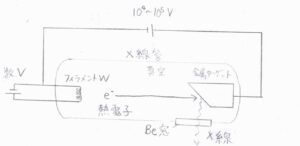
融点の高いタングステン(\(\rm{W}\))などの金属でできたフィラメントに数\(\rm{V}\)の電圧をかけて、電子を真空に飛び出させます。
この電子に\(10^4\sim 10^5\ \rm{V}\)という高電圧をかけることで、電子を一気に加速させます。
加速した電子は、陽極側に設置された銅などの金属と衝突し、このときにX線が発生します。
発生したX線は、透過性の高いベリリウム(\(\rm{Be}\))などでできた窓を通って、真空管の外へと出ていきます。
そして、この装置によって発生するX線の強度は、下のグラフのようになることが知られています。

縦軸がX線強度、横軸はX線の波長です。
まず、鋭いピークは、外殻側にある電子が内殻側へと緩和することによるもので、特性X線と呼ばれます。
特性X線の波長は、ポテンシャルの差によって決まるため、元素に依存することになります。
高圧電源の電圧には依存しません。
一方、広い周波数範囲にわたって発生する比較的弱いX線は、連続X線と呼ばれます。
金属ターゲットの原子核による電場の影響で、電子の進行方向が曲がり、制動放射が起こります。
電子がどれくらい原子核の近くを通るかによって、光子のエネルギーに違いが出るため、広い周波数範囲にわたるX線が発生します。
発生するX線のエネルギーは、電子のエネルギーよりも大きくなることはないため、連続X線は最小の波長の値を持ちます。
ただし、ここで紹介したのはX線を発生させる方法の一例にすぎず、より強いX線も発生させられるシンクロトロン放射線源が使われることもあります。
ブラッグの法則
続いて、高校物理で習うブラッグの法則について、おさらいをします。
異なる結晶面によって反射されたX線は、その波長と反射する角度によって、強め合ったり弱めあったりします。
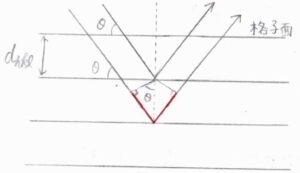
強め合いが起こるための条件式は、\(2d_{hkl}\sin{\theta}=n\lambda\)で与えられます。
ここで、\(d_{hkl}\)は\(\{h\ k\ l\}\)面の間隔、\(\theta\)は入射X線の進行方向と結晶面がなす角度、\(n\)は自然数で、\(\lambda\)はX線の波長です。
\(2d_{hkl}\sin{\theta}\)は、図の中で赤線の長さを表しており、これが波長の自然数倍であれば、異なる結晶面によって反射された光どうしが干渉して強め合うということです。
\(n\)は、経路差が波長いくつ分であるかという値で、回折次数と呼ばれます。
この条件式により、波長が既知のX線を結晶に反射させて、強め合いが起こる角度を調べれば、結晶面の間隔を計算によって求めることができます。
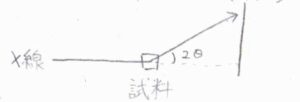
ただし、実験的には\(\theta\)そのものではなく、視射角\(2\theta\)を記録するのが普通です。
そして、この条件式を両辺を\(n\)で割ると、\(\displaystyle 2\frac{d_{hkl}}{n}\sin{\theta}=\lambda\)となりますが、ここで前回求めた格子面の間隔の式を使います。
前回の記事はこちら

ミラー指数をすべて\(n\)倍してよいものとすると、格子面の間隔が\(\displaystyle \frac{1}{n}\)倍になることから、ブラッグの法則は\(2d_{nh, nk, nl}\sin{\theta}=\lambda\)とも表すことができます。
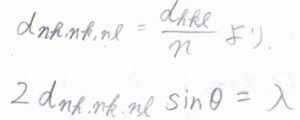
ラウエ条件(ラウエの式)
それではここから、X線によって結晶構造を調べる一般的な方法について、お話ししていきます。
図のように、結晶にX線を当てて、その先にX線感光フィルムを置くと、周期的に繰り返された結晶構造が回折格子と同じはたらきをして、1列に並んだ点を浮かび上がらせます。
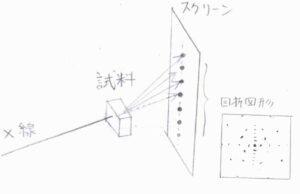
このとき、回折が起こる結晶面は1つではないため、さまざま角度を変えながら、点が発生します。
このようにしてできた模様は、回折図形と呼ばれます。
普段、我々が小さいものを見るときには、虫眼鏡や顕微鏡を使いますが、X線はとても高い透過性をもつため、結像できるほどのレンズを作ることができません。
そのため、この回折図形をもとにして、計算によって結晶構造を求めることになります。
ただし実験的には、強め合いが起こる角度だけでなく、反射光の強度も計算に必要であるため、検出器を動かしながら、角度と強度を記録していくことになります。
ここで、回折光の強め合いが起こるための条件式を紹介します。
導出過程は次の記事でお話しするので、ここでは結果だけを示します。
まず、入射光と回折光の波数ベクトルをそれぞれ\(\boldsymbol{k}_\rm{i}\)、\(\boldsymbol{k}_\rm{o}\)とします。
ここでは、回折しても波長はそのままであると仮定しています。
そして、繰り返し構造の間隔を\(r\)とします。
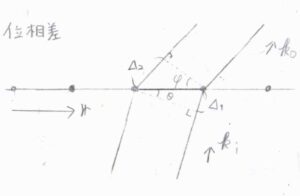
さらに、図のように2つの角度を\(\theta\)、\(\varphi\)とおきます。
図の中で、入射光と回折光の経路差は、\(\Delta_2-\Delta_1\)であり、これは\(r\sin{\varphi}-r\sin{\theta}\)で与えられます。

位置ベクトル\(\boldsymbol{r}\)における入射光の位相\(\boldsymbol{k}_\rm{i}\)\(\cdot \boldsymbol{r}\)は、\(kr\sin{\theta}\)であり、これは\(\displaystyle \frac{2\pi}{\lambda}\Delta_1\)に相当します。

回折光の位相も、\(\displaystyle \frac{2\pi}{\lambda}\Delta_2\)と等しいため、入射光と回折光の位相差は\((\boldsymbol{k}_\rm{o}\)\(-\boldsymbol{k}_\rm{i}\)\()\cdot \boldsymbol{r}\)と表されます。
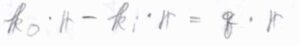
\(\boldsymbol{k}_\rm{o}\)\(-\boldsymbol{k}_\rm{i}\)は散乱ベクトルと呼ばれるもので、これを\(\boldsymbol{q}\)と表すことにすると、X線の回折条件は、\(\boldsymbol{q}\cdot \boldsymbol{a}=2\pi h\)、\(\boldsymbol{q}\cdot \boldsymbol{b}=2\pi k\)、\(\boldsymbol{q}\cdot \boldsymbol{c}=2\pi l\)、これら3つの式が成り立つ\(\boldsymbol{q}\)で強め合いが起こるということになります。
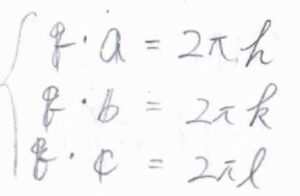
この条件式をラウエ条件あるいはラウエの式と言います。
ここで、\(\boldsymbol{a}\)、\(\boldsymbol{b}\)、\(\boldsymbol{c}\)は結晶格子の基本ベクトル、\(h\)、\(k\)、\(l\)は整数であり、ラウエ指数と呼ばれます。
ラウエ指数とミラー指数の違いは、次回の記事を参照してください。
ラウエ条件を満たすのは、\(\displaystyle \boldsymbol{q}=\frac{2\pi}{V}(h\boldsymbol{b}\times \boldsymbol{c}+k\boldsymbol{c}\times \boldsymbol{a}+l\boldsymbol{a}\times \boldsymbol{b})\)のときであり、このベクトルは逆格子ベクトルと呼ばれます。
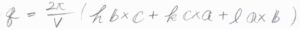
ここで、\(V\)は3つの基本ベクトルによってできる平行六面体の体積で、\(\boldsymbol{a}\cdot (\boldsymbol{b}\times \boldsymbol{c})\)で与えられます。
もちろん、\(V=\boldsymbol{b}\cdot (\boldsymbol{c}\times \boldsymbol{a})\)、\(V=\boldsymbol{c}\cdot (\boldsymbol{a}\times \boldsymbol{b})\)などと書いても問題ありません。
原子散乱因子
以上が、強め合いが起こる角度についての話でしたが、ここからは回折光強度についても、その物理的な意味を考えていきます。
そもそもX線の散乱は、入射X線が原子内の電子を振動させることによって起こります。
そのため、原子番号が大きい元素であるほど、X線を強く散乱させることになります。
1つの原子の散乱振幅への寄与は、\(\displaystyle \int \rho(\boldsymbol{r})\exp{(\rm{i}\mathit{\boldsymbol{q}\cdot \boldsymbol{r}})}\rm{d}\)\(\tau\)と定義され、これを原子散乱因子と言います。
ここで、\(\rho(\boldsymbol{r})\)は電子密度分布です。
\(\exp{(\rm{i}\mathit{\boldsymbol{q}\cdot \boldsymbol{r}})}\)の部分は、電子の位置の違いからくる位相の差を調整するものです。

内積の計算で必要な散乱ベクトルの大きさ\(q\)は、こちらのように余弦定理で求めることができて、\(\displaystyle \frac{4\pi}{\lambda}\sin{\theta}\)で与えられます。
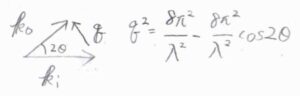
いまは原子について考えているため、電子密度が球対称であるとすると、変数を1つに減らすことができます。
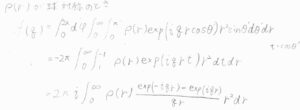
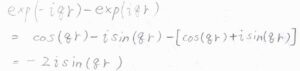
その結果、散乱因子\(\displaystyle f(q)=4\pi\int_0^\infty \rho(r)\frac{\sin{qr}}{qr}r^2\rm{d}\)\(r\)となります。
特に、\(\theta\rightarrow 0\)のときには、\(\displaystyle \frac{\sin{qr}}{qr} \rightarrow 1\)となるため、\(f(q)\)は原子がもつ電子の総数と一致します。

縦軸に\(f\)、横軸に\(\displaystyle \frac{\sin{\theta}}{\lambda}\)をとると、こちらのグラフのようになります。

視射角が限りなく\(0\)に近いところでは、酸素原子は水素原子の\(8\)倍、散乱光の振幅へ寄与するということです。
結晶構造因子
さらに、単位胞に含まれるすべての原子やイオンの寄与を考えることで、回折光の全振幅への寄与を求めることができます。
これを結晶構造因子と言います。
それぞれの原子中心の座標を\((x_ja, y_jb, z_jc)\)とすると、結晶構造因子\(\displaystyle F_{hkl}=\sum_jf_j(\boldsymbol{q})\exp{[2\pi \rm{i} (\mathit{hx_j+ky_j+lz_j})]}\)と書けます。
ここで、\(a\)、\(b\)、\(c\)は辺の長さを表す格子定数です。
\(h\)、\(k\)、\(l\)はラウエ指数です。
結晶全体で回折光への寄与を考える場合には、さらにすべての単位胞について、和をとることになりますが、ここについては次回お話しすることにします。
電子密度の計算方法
そして、最後に回折が起こったときの角度と回折光の強度から、いかにして結晶構造を計算するのかという話をします。
まず、電子密度\(\rho(\boldsymbol{r})\)はフーリエ合成という操作によって、構造因子から逆算することができます。
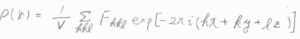
これまでやってきた、位相差を考慮しながら足し合わせるという計算は、偶然にもフーリエ変換という数学的な操作と同じであり、逆フーリエ変換によって元の関数に戻すことができます。
ただ、ここで1つ大きな問題があります。
古典的には、回折光強度は振幅の二乗に比例するため、強度の平方根から電子密度まで計算できます。
しかし実際には、構造因子は複素数となることもあるので、大きさはわかっても、実験結果からその値を一意的に決定することができません。
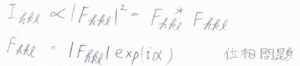
この不確定性のことを位相問題と言います。
もし構造因子の位相を間違えれば、得られる電子密度分布も大きく異なったものになるため、位相問題を克服する数学的手法が数多く提案されてきました。
複雑な計算を要するため、とても手計算できるようなものではなく、コンピュータに計算させます。
現在は、実験装置に実装されて、それらもほぼ自動化されており、タンパク質のように巨大な分子についても、もっともらしい構造を割り出すことがなされています。
(ちなみに、タンパク質の場合は、そもそも結晶化させることが難しいので、X線を当てる段階にたどり着くまでに、多くの実験が必要になります。
決定された構造は、PDBで閲覧することができます。)
処理の方法をいくつか紹介すると、まずパターソン合成という方法では、構造因子の代わりに、不確定性がない回折光強度をそのままフーリエ合成の式に入れて、電子密度に似た関数である\(P(\boldsymbol{r})\)を得るという方法です。
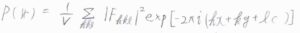
続いて、重原子法というのは、重い原子ほど散乱強度が大きいことを利用する方法です。
結晶が原子番号の大きな原子を含んでいると、構造因子の位相をその原子のみの位置から予想しても、そこまで実際の値と差が出ません。
3つ目の直接法は、反射間の関係や電子密度への制約条件をもとに、統計学的にもっともらしい結晶構造を割り出す方法です。
測定によって位相の情報が消えるといっても、ミラー指数の異なる2つの構造因子の位相に関係を見出すことが可能であり、そこから位相を予想します。
最終的には、原子の位置を微妙に変えながら、最も実験結果と合致する結晶構造を見つけることになります。
前の2つの方法に比べると、直接法は膨大な計算を必要とするため、コンピュータ技術とともに発展し、重原子を含まない分子の結晶やタンパク質などの巨大な分子の構造解析に使われるようになっていきました。
今回紹介した方法以外にも計算方法はあって、タンパク質の解析では分子置換法や重原子同型置換法などの方法が使われています。
練習問題
それでは最後に、前回お話しした内容の練習問題をやって、終わろうと思います。
2種類のイオンが互いに侵入した面心立方格子の形をとる\(\rm{NaCl}\)結晶にX線を照射したとき、回折光が観測されないときの条件はどのようになるでしょうか?
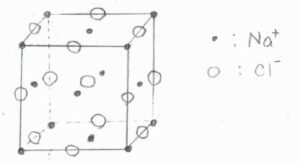
次に、1つの単位胞について、この図のように、1つの頂点を原点とした座標を考えます。

頂点にある\(\rm{Na}^+\)については、\(\displaystyle \frac{1}{8}\)の部分しか単位胞に含まれていないので、その寄与は\(\displaystyle \frac{1}{8}f^+\)だと考えます。
そうすると、結晶構造因子\(F_{hkl}\)の第一項は、こちらのように書くことができます。
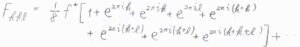
オイラーの公式より、整数\(n\)として\(\rm{e}\)\(^{2\pi \rm{i}\mathit{n}}=1\)であるため、大かっこの中は\(8\)だとわかります。
同様に、面の中心にある\(\rm{Na}^+\)の寄与を\(\displaystyle \frac{1}{2}f^+\)、辺の中点にある\(\rm{Cl}\)\(^-\)の寄与を\(\displaystyle \frac{1}{4}f^-\)とすると、\(F_{hkl}\)はこちらのように表されます。
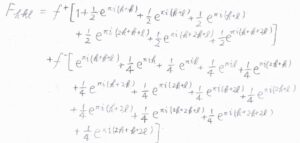
\(\rm{e}\)\(^{\pi \rm{i}}=-1\)であることを利用して変形すると、
\( F_{hkl}=f^+[1+(-1)^{h+k}+(-1)^{k+l}+(-1)^{h+l}]+f^-[(-1)^{h+k+l}+(-1)^h+(-1)^k+(-1)^l]\)となります。
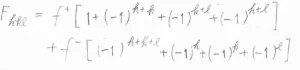

仮に\(h\)、\(k\)、\(l\)がすべて偶数だったとすると、\(F_{hkl}=4f^++4f^-\)となります。
すべて奇数のときには、\(F_{hkl}=4f^+-4f^-\)となります。
\(\rm{Na}\)\(^+\)と\(\rm{Cl}\)\(^-\)の電子数はそれぞれ\(10\)個と\(18\)個で異なり、明らかに\(f^+\)と\(f^-\)は等しくないため、これも\(0\)ではない値となります。
一方で、\(h\)、\(k\)、\(l\)のうち、1つだけが奇数の場合を考えると、かっこの中がいずれも\(0\)であるため、\(F_{hkl}=0\)となります。
2つだけが奇数の場合も\(F_{hkl}=0\)となります。
\(F_{hkl}=0\)のとき、回折光の強度も\(0\)となるため、対応する反射が観測されないことになります。
このように、ブラべ格子の種類によって、特定の\(\{h\ k\ l\}\)面からの反射が観測されなくなることが知られており、その法則のことは消滅則と言います。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




