こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
それでは内容に入っていきます!
ガウス鎖モデルの問題点
始めに、ガウス鎖および酔歩鎖ではすべての実在高分子を表現できない理由についてお話しします。
ガウス鎖、酔歩鎖については、こちらを参照してください。

二次元酔歩鎖を例にすると、投げたコインの表裏に合わせて、ふらふらと動いていくわけですが、そのとき、このようにすでに1回通った格子点をもう一度通ることがあります。
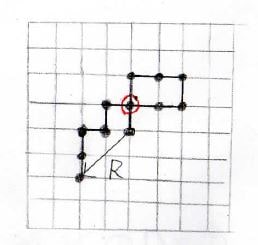
酔歩鎖のモデルではモノマーの大きさを考えずに常に全方向へ等確率で進んでいくことを考えているため、こういった場合も含めて平均量を計算していますが、現実には立体反発が起こるため、こういうループ構造は排除してから平均をとるべきです。
このようにループ構造が不安定化する効果を排除体積効果と呼び、特にいまは希薄溶液を考えているため、分子内排除体積効果と言います。
隣接する内部回転角の相関によって分子が広がるペンタン効果に対して、この排除体積効果はいくつもの内部回転角の組み合わせの不安定性を考えているので、長距離の相互作用であると言えます。
(ペンタン効果についても、上記の記事でお話ししております。)
そして、考えられるすべての場合からループを排除した高分子モデルは自己回避鎖と呼ばれます。
自己回避鎖の回転半径は、排除体積効果を考えていないガウス鎖の値よりも大きくなり、その比は半径膨張因子と呼ばれます。
ガウス鎖と自己回避鎖の両末端間距離の分布は下のようになり、\(R\)が小さいときには排除体積効果が顕著に効いてくるため、存在確率が下がり、逆に\(R\)が大きいときの確率が上がります。

導出は少し難しいですが、排除体積効果を考えた屈曲性高分子の平均二乗回転半径はモノマー数の\(1.2\)乗になることが知られています。
ガウス鎖だと\(n\)の\(1\)乗に比例するはずなので、この指数でどちらか判別することができます。
そしてこの半径膨張率\(\alpha_S\)は、下の式で定義する排除体積パラメータ\(z\)の関数になります。
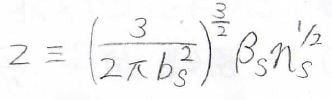
ここで\(n_S\)と\(b_S\)は、高分子セグメントの個数と結合長です。
セグメントというのは、小さな構成要素という意味で、これまでは主鎖の原子だけを考えていましたが、いくつかの主鎖の原子をまとめたり、側鎖の原子も含めたりした原子よりも大きな塊を指します。
とは言っても抽象的でわかりにくいので、ここではモノマー単位のことだと思っていただいても問題ありません。
そして、\(\beta_S\)は定数です。
縦軸を\(\alpha_S^2\)、横軸を\(\displaystyle z^{\frac{2}{5}}\)としてグラフを書くと、下のようになることが知られていますが、実際の関数の導くことは数学的にかなり難解で、シミュレーションから求めた近似式や実験から得られた経験式しかありません。
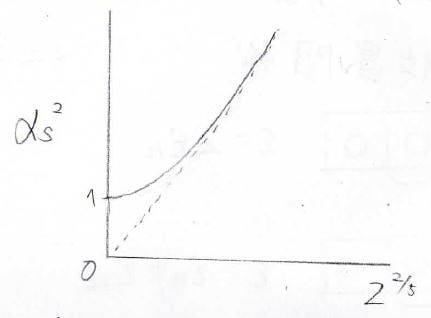
そして、このグラフを見ると、\(z\)が小さいときには\(\alpha_S\)がほぼ\(1\)になるため、ガウス鎖として考えても問題ないことになります。
この\(z\)が小さくなるというのはつまり、排除体積効果によって生まれるセグメント間の斥力に対して、何らかの引力がはたらいている状態を表しています。
その斥力と引力のバランスにあたるのが、先ほど定数と紹介した\(\beta_S\)で、これを2体クラスター積分と呼びます。
良溶媒と貧溶媒
それでは高分子にはたらく引力とはなんのことでしょうか?
ここで重要になるのが高分子と溶媒の親和性です。
親和性が高く、その高分子をよく溶かす溶媒は良溶媒、親和性が低く、その高分子をあまり溶かさない溶媒は貧溶媒と呼ばれます。
各溶媒中での高分子のコンフォメーションを考えると、下の図のようになります。
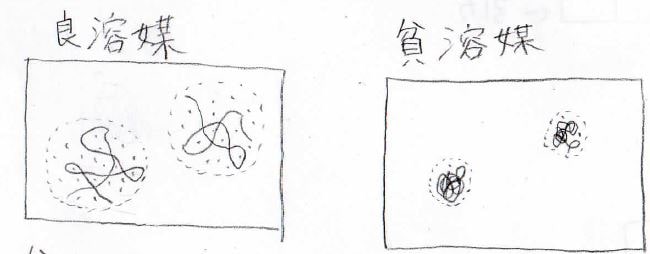
左の良溶媒中では高分子と溶媒の親和性が高いため、糸毬状に広がった高分子の球の中にたくさんの溶媒分子が入り込みます。
対して貧溶媒中では、高分子と溶媒の親和性が低いので近くに溶媒分子を置くよりも、自分自身のセグメントを置いた方が熱力学的に安定になります。
その結果、このように縮まった構造をとるようになります。
この縮もうとする力こそが、排除体積効果と対をなす引力になります。
2体クラスター積分
それではどうやって斥力と引力のバランスを考えるのか、格子モデルを使って説明します。
これから図で説明しますが、図中で●を高分子のセグメント、○を溶媒分子とします。
また、高分子セグメントに\(1\)、溶媒分子に\(2\)という番号を付けて表すことにします。
引力を考えるうえで重要なのは、セグメント同士が近づいたときにどれくらいエネルギーが安定化するのかということです。
下図の下側のように格子内でセグメント同士が隣接した状態が最も安定であるとすると、その直前の状態は、間に1個溶媒分子が入った、上側の形になります。

\(\varepsilon_{12}\)を高分子セグメントと溶媒が隣接したときのポテンシャル、同じく\(\varepsilon_{11}\)を高分子セグメント同士、\(\varepsilon_{22}\)を溶媒同士のポテンシャルとするとこの2つの状態間エネルギー\(\Delta \varepsilon\)は\(\varepsilon_{11}+\varepsilon_{22}-2\varepsilon_{12}\)となります。
この値が負に大きいほど、大きな引力がはたらくことになります。
そして、セグメント間距離を\(r\)、ポテンシャルエネルギーを\(u(r)\)とすると、このグラフのようになります。
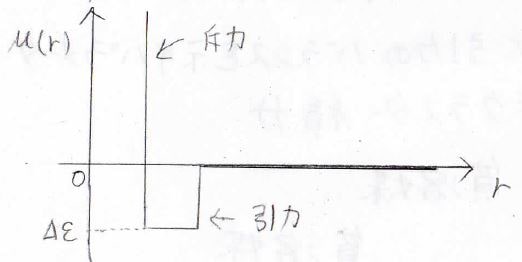
ここで、\(r\)が小さいときに\(u(r)\)が無限大になっているのは、排除体積効果による斥力、\(\Delta \varepsilon\)の分だけ谷になっているのが、引力を表しています。
ここで、斥力と引力を受けるセグメントの割合を、ボルツマン分布から考えるために、縦軸を\(\displaystyle 1-\exp{[-\frac{u(r)}{k_BT}]}\)とすると、こんなグラフになります。
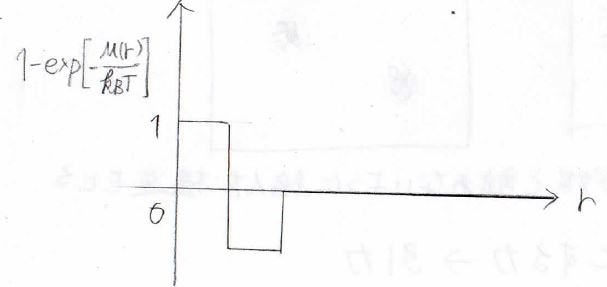
そして、2体クラスター積分\(\beta_S\)は、これを\(r\)について積分した値として定義されます。
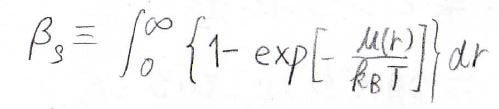
シータ状態
良溶媒では\(\beta_S\)は大きく、排除体積効果がはたらきますが、貧溶媒では\(\beta_S\)が小さくなるため、排除体積効果があまり効かなくなります。
そして、\(\beta_S\)がちょうど\(0\)になったときには、排除体積効果が無視できるようになり、この状態をシータ状態、そのときの溶媒をシータ溶媒と言います。
\(\beta_S\)は温度に依存するため、シータ状態は高分子と溶媒の組み合わせだけでなく、絶妙な温度によって達成されます。
\(34.5^\circ \rm{C}\)のポリスチレンシクロヘキサン溶液がその一例で、このときには平均二乗回転半径がモノマー数に比例し、ガウス鎖としてみなすことができます。
このときには、見かけ上、高分子セグメントは大きさをもたないという面白い状態になります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




