こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(entropy change)
それでは内容に入っていきます!
外界
まずは、ある系から外界へ熱が逃げていったときの、外界のエントロピー変化\(\Delta S\)を考えます。
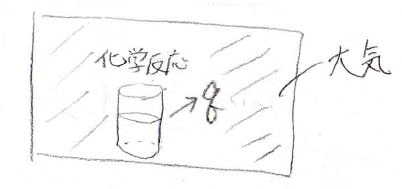
変化が起こっている系と周りの大気をまとめて孤立系とみなすことで、エントロピー増大則が適用できるため、外界のエントロピー変化を考えることは、自発性の議論に不可欠なものとなります。
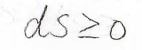
エントロピー増大則については、こちらを参照してください。

そして、外界は体積がとても大きいので、少し熱を受け取ったくらいの体積変化なら無視できます。
体積変化がないということは、仕事がないということなので、熱力学第一法則より、内部エネルギーの変化量\(\rm{d}\)\(U\)は系に与えられた熱量\(\rm{d’}\)\(q\)と等しいと考えることができます。
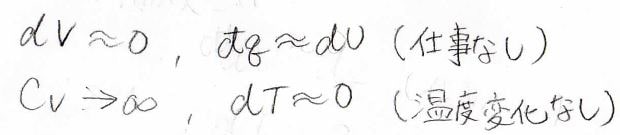
また、示量性の状態量である体積が大きいということは、物質量が大きいということであるため、同じく示量性の定積熱容量\(C_V\)もとても大きいはずです。
熱容量が大きいということは、温度が変化しにくいということであるため、温度変化\(\rm{d}\)\(T\)は無視できるほど小さいと考えることができます。
ここで、エントロピーの熱力学的な定義より、\(\rm{d}\)\(\displaystyle S\geq \frac{\rm{d}\mathit{U}}{T}\)となりますが、エントロピーと内部エネルギーはともに状態量であるため、変化の経路によらず一意的に決まります。
つまり、その変化の経路が可逆か不可逆かに関係なく、常に等号が成り立ちます。
積分のときには、\(T\)をそのまま外に出すことができて、\(\displaystyle \Delta S=\frac{q}{T}\)となります。
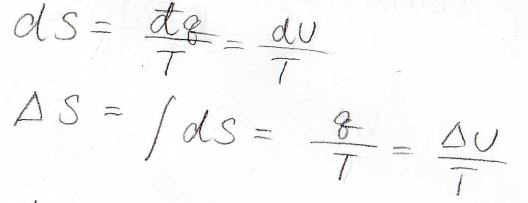
熱溜まりがなく、全体が均一な温度だった場合は、熱の移動が起こらないので\(\Delta S=0\)、すなわち外界のエントロピーは一定ということになります。
理想気体の等温変化
続いて、理想気体の等温変化を考えてみましょう。
温度が\(T\)で一定のまま、圧力と体積がそれぞれ\(p_1\)から\(p_2\)、\(V_1\)から\(V_2\)へ変化したとします。
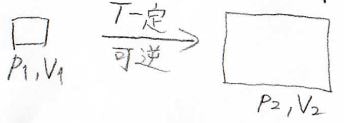
理想気体の内部エネルギー\(U\)は、温度と物質量のみで決まるため、等温変化では一定です。
そして、体積変化が十分にゆっくり起こったとしたとき、系に与えられた仕事\(w\)は\(-p\rm{d}\)\(V\)の定積分として表されます。
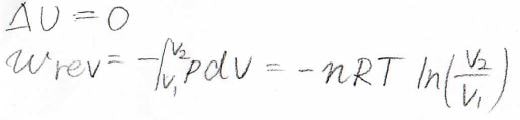
理想気体の状態方程式より\(\displaystyle p=\frac{nRT}{V}\)となるため、この積分は\(\displaystyle -nRT\ln{(\frac{V_2}{V_1})}\)となります。
内部エネルギーが一定であることと熱力学第一法則より、熱量\(q=-w\)となるので、\(\displaystyle q=nRT\ln{(\frac{V_2}{V_1})}\)と計算されます。
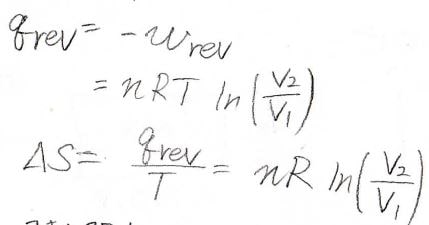
エントロピー変化\(\Delta S\)は、これを\(T\)で割った値であるため、\(\displaystyle nR\ln{(\frac{V_2}{V_1})}\)となります。
この符号は、\(V_1\)と\(V_2\)の大小関係によって決まるもので、膨張はエントロピーの増大、収縮はエントロピーの減少に対応します。
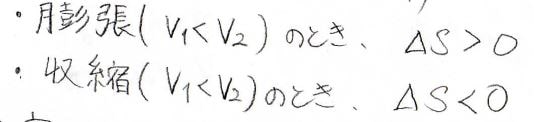
理想気体の定圧変化
それでは定圧変化ではどうなるでしょうか?
ここでは、圧力が\(p\)で一定、温度が\(T_1\)から\(T_2\)まで変化したとします。

圧力一定条件下において、系が与えられた熱量は、エンタルピーの変化量に相当しますから、これを利用します。
理想気体であれば、ジュール-トムソン係数が\(0\)なので\(\rm{d}\)\(H=C_p\rm{d}\)\(T\)となります。
ここで、\(C_p\)は定圧熱容量です。
ジュール-トムソン係数については、こちらを参照してください。

したがって、エントロピー変化\(\Delta S\)は、こちらの積分で求められることになります。

ここで、\(C_p\)の温度依存性を無視した場合には、定数として積分の外に出せて、\(\displaystyle \Delta S=C_p\ln{(\frac{T_2}{T_1})}\)と表すことができます。
よって、温度が上昇したときにはエントロピーは増大、温度が低下したときにはエントロピーが減少することになります。
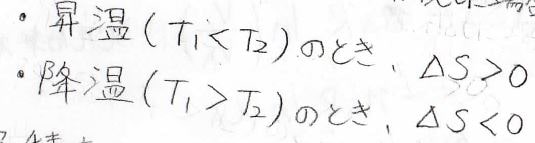
理想気体の定積変化
また、定積変化については、系に与えられた微小な熱量\(\rm{d’}\)\(q\)が内部エネルギー変化\(\rm{d}\)\(U\)に相当し、定積熱容量\(C_V\)として\(C_V\rm{d}\)\(T\)となります。
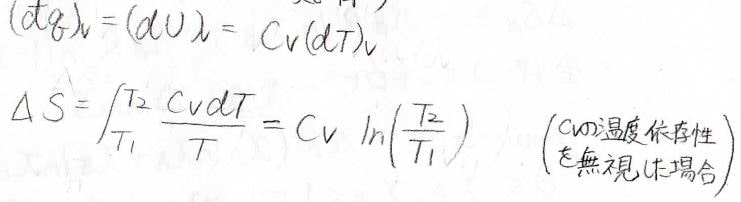
定圧変化と同様に計算できて、\(C_V\)の温度依存性を無視した場合には、\(\displaystyle \Delta S=C_V\ln{(\frac{T_2}{T_1})}\)となります。
2種類の理想気体の混合
それでは最後に、2種類の理想気体が混ざることによるエントロピー変化を考えてみましょう。
考えるのは、下のような系です。
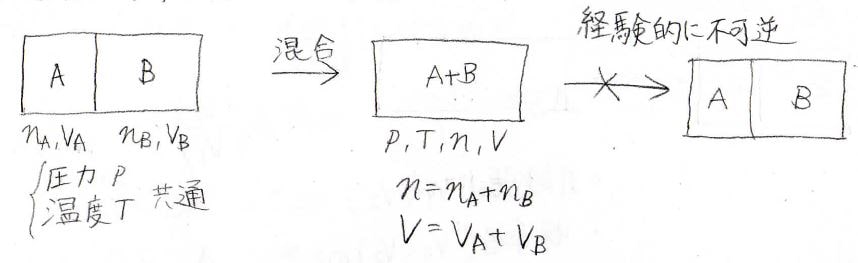
圧力と温度が同じで物質量がそれぞれ\(n_\rm{A}\)、\(n_\rm{B}\)である2つの理想気体\(\rm{A}\)と\(\rm{B}\)があります。
それぞれの体積は\(V_\rm{A}\)、\(V_\rm{B}\)としておきます。
そして、この間の仕切りを外して、気体が完全に混ぜるまで放置します。
すると、全体の圧力と温度はそのまま、物質量は\(n_\rm{A}\)\(+n_\rm{B}\)となります。
この全体の物質量は\(n\)とし、全体の体積を\(V\)としておきます。
すると、混合する前と後で、温度は変化していないので、理想気体であれば内部エネルギーは変化していないことになります。
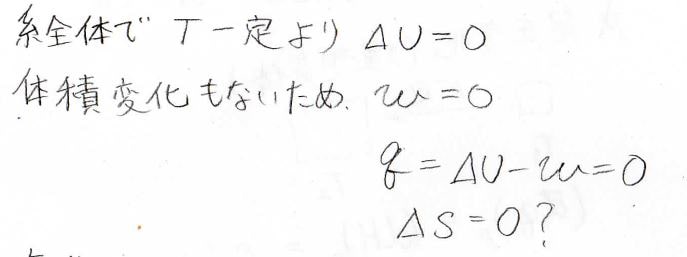
また、全体の体積も一定なので、系がされた仕事はありません。
したがって熱力学第一法則より、系に与えられた熱量も\(0\)になります。
等温過程におけるエントロピー変化は、熱量を温度で割った値であるため、エントロピー変化も\(0\)になりはずです。
しかし、よく考えてみると、一度完全に混ざってしまった気体が、再び自然に分かれることはないので、気体の混合は不可逆な変化と言えます。
すると、エントロピーは増大するはずなので、矛盾が生じます。
ここで、出てくるのが分圧の考え方です。
気体\(\rm{A}\)にのみ着目した場合には、等温膨張とみなすことができます。
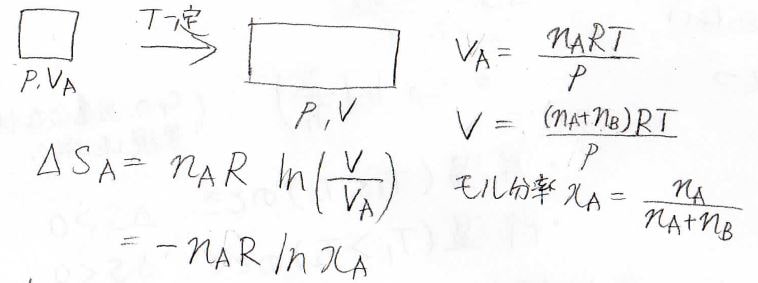
このとき、体積は\(V_\rm{A}\)から\(V\)へ変化し、気体\(\rm{A}\)の分圧\(p_\rm{A}\)\(\displaystyle =\frac{n_\rm{A}}{n_\rm{A}+\mathit{n}_\rm{B}}p\)となります。
これをもとにエントロピー変化を積分によって求めると、\(\Delta S=n_\rm{A}\)\(R\ln{(\frac{n_\rm{A}+\mathit{n}_\rm{B}}{n_\rm{A}}})\)となります。
気体\(\rm{A}\)のモル分率を\(x_\rm{A}\)とすると、\(\Delta S=-n_\rm{A}\)\(R\ln{x_\rm{A}}\)と書き表すこともできます。
同様に気体\(\rm{B}\)についてのエントロピー変化も計算することができて、モル分率を\(x_\rm{B}\)とすると、\(\Delta S=-n_\rm{B}\)\(R\ln{x_\rm{B}}\)となります。
したがって2種類の気体が混合することによる全体のエントロピー変化は、\(-nR(x_\rm{A}\)\(\ln{x_\rm{A}}\)\(+x_\rm{B}\)\(\ln{x_\rm{B}})\)となります。
ここで、モル分率\(x\)は\(0\)より大きく\(1\)未満の値をとるため、\(\ln{x}\)の部分はどちらも負の値となります。
つまり、\(\Delta S\)は正の値をとります。
このことは、実際に熱の出入りがなかったとしても、不均一なものが均一に混ざるという現象でエントロピーが増大するということを示しています。
この混合に伴うエントロピー変化のことは、そのまま混合エントロピーと言います。
エントロピーの増大があるのは、特に気体に限った話ではなく、例えば、溶質と溶媒という2種類以上の物質からなる溶液や、複数の金属が混ざってできる合金をつくるときなども当てはまります。
詳しくは、こちらの記事をご参照ください。


まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




