こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(hydrogen calculus of variations)
変分法の流れ
まず変分法とは、シュレディンガー方程式が厳密に解けない多体問題を扱うテクニックの1つです。
始めに、解として得られる波動関数の大まかな形を予想して、未知数を含む形の関数を作ります。
この関数のことは、試行関数と言います。
そして次に、この試行関数を未知数を含んだままの形でシュレディンガー方程式に入れてエネルギーを求めます。
しかし、このエネルギーにも未知数が残っているので、最後にその未知数を消去します。
自然界は低いエネルギー状態をとるはずなので、エネルギーが極小となるような未知数を代入することで、波動関数とエネルギーが求められます。
水素原子の基底状態
実際にやってみましょう。
今回は、水素原子の基底状態を考えていきます。
水素原子のシュレディンガー方程式についてはすでに解説しましたが、改めて変分法で考えてみます。
計算方法
基底状態でのハミルトニアンは、下の形になります。
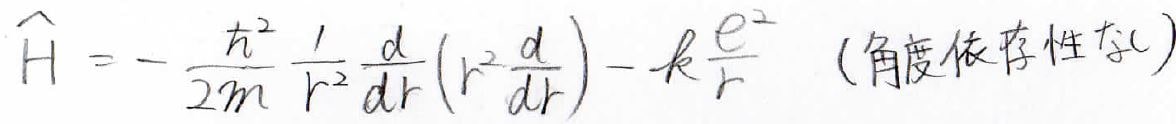
極座標で書いていますが、角度依存性がないので、変数は\(r\)だけになってます。
そして、いちばん重要な試行関数ですが、長距離側の極限を考えると指数関数型の減衰関数であることが予想できるので、このようにおきます。
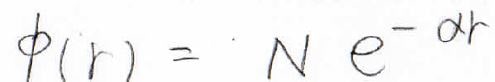
\(N\)が規格化定数で、\(\alpha\)が未知数です。
この予測については、水素原子についてシュレディンガー方程式を解いた記事が参考になります。
試行関数を作ったら、これをシュレディンガー方程式に入れてみます。

この式の両辺に\(\phi^\ast\)を左からかけて全空間で積分し整理すると、エネルギーがこの形で求められることがわかります。
この式は、別の表現をされることもあるので知っておいてください。
右の形は、ブラケット表示と言います。
シュレディンガー方程式の意味についてはこちらで解説しています。

では、実際にエネルギーを出してみましょう。
規格化
まず規格化して、分母が\(1\)になるようにします。
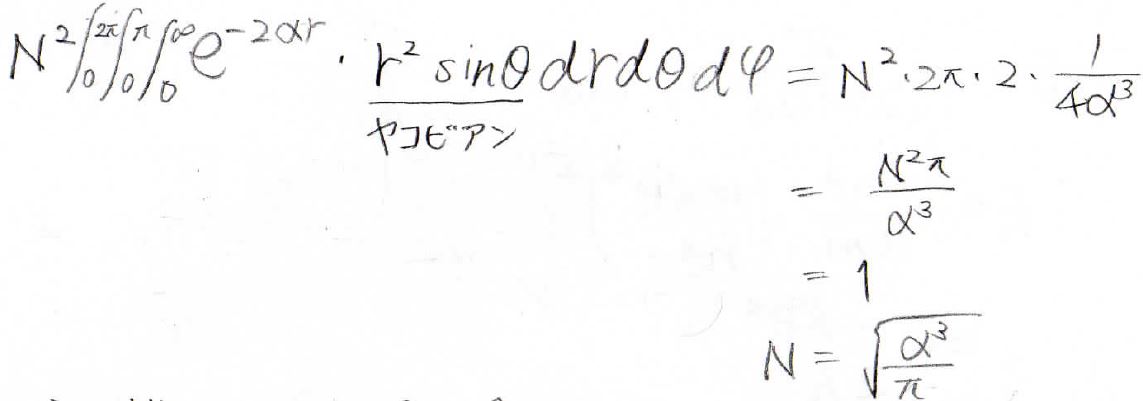
ヤコビアンも入れて計算していくと、\(N=\displaystyle \sqrt{\frac{a^3}{\pi}}\)になりました。
ヤコビアンについてはこちらをご覧ください。

エネルギー
では今度、分子の部分を見ていきます。
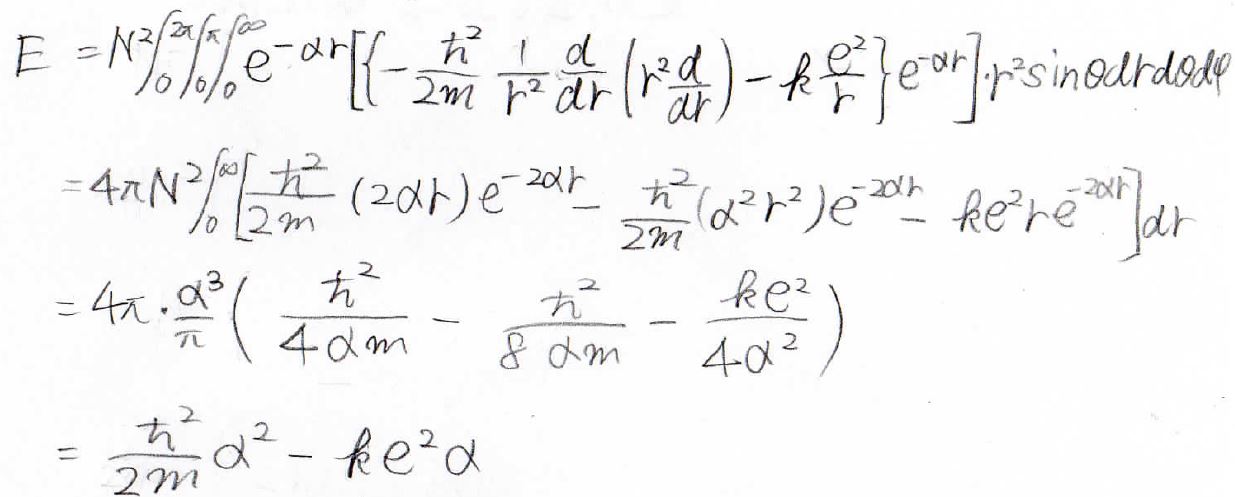
エネルギーを未知数\(\alpha\)を含む形で求めることができました。
エネルギーの極小
最後に、安定な部分、すなわちエネルギーが極小をとる部分を探します。
極小では\(\alpha\)での微分が\(0\)になります。
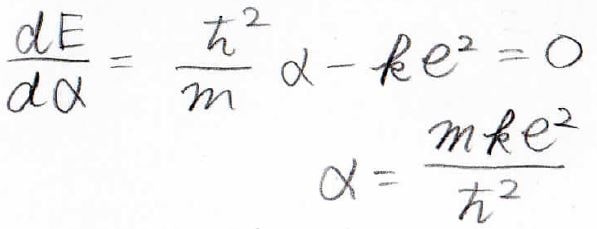
これを変形することで、未知数\(\alpha\)が求められました。
この\(\alpha\)を試行関数とエネルギーの式に入れると、それらを値として求めることができます。
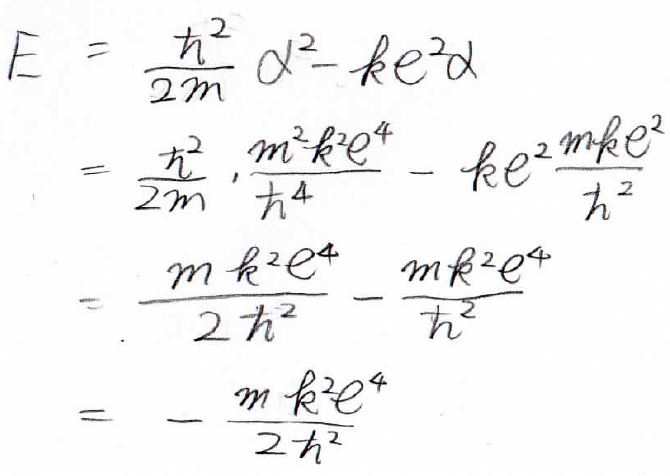
結果として、\(\displaystyle E=-\frac{mk^2e^4}{2\hbar^2}\)となりました。
シュレディンガー方程式、ボーアのモデルとの比較
計算されたエネルギーをシュレディンガー方程式から解いたエネルギーと比較してみると、ボーア半径が\(\displaystyle \frac{\hbar^2}{mke^2}\)で与えられることから、変分法で求めたものと同じ値になっていることが確認できます。

水銀原子の軌道計算についてはこちらをご覧ください。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




