こんにちは!
今回も行列の話の続きやっていきます。
今日のテーマはこちら!
単位行列については、行列の第一弾の記事で少し触れましたが、まだ掛け算の話をしていなかったので、改めて説明していきます。
動画はこちら↓

動画で使ったシートはこちら(inverse matrix)
それでは内容に入っていきます。
単位行列
まず、単位行列についてお話しします。
単位行列は正方行列の1つであり、主対角線上の成分がすべて\(1\)で、それ以外の成分がすべて\(\displaystyle 0\)の行列を指します。
単位行列とある\(n\)次正方行列のかけ算には、このような関係が成り立っています。

単位行列をかけても、元の行列と同じものになります。
また、かける順番を交換してもこの関係は成り立ちます。
一般的に、行列のかけ算は交換できないので、これは特殊な例になります。
転置行列
続いて紹介するのは、転置行列です。
これは、ある行列\(\bf{\rm{A}}\)があったときに、その\((i,j)\)成分が\((j,i)\)成分になるように成分を並べ替えた行列です。
\(\bf{\rm{A}}\)の転置行列は、\(\bf{\rm{A}}\)の左上に小文字の\(t\)をつけて\(^t\bf{\rm{A}}\)と表します。
また、大文字の\(T\)を右上に書く表記など、そのほかにもいくつか表記の仕方が知っておいてください。
例えば、下の行列の転置行列は、このようになります。
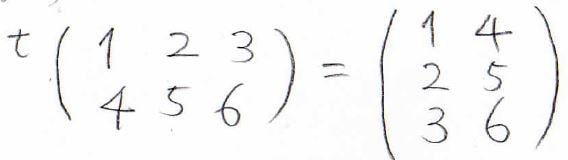
行と列の数が入れ替わっているので、横に長い行列の転置行列は、縦長の行列になります。
転置の演算
転置をとる操作には次のような法則があるので、知っておいてください。
まず、\(\bf{\rm{A}}+\bf{\rm{B}}\)をまとめて転置をとったものは、それぞれの転置行列の和と等しくなります。
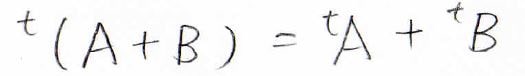
そして、\(\bf{\rm{AB}}\)という行列の積に対して転置をとった場合には、行列の順番が入れ替って、\(^t\bf{\rm{B}}\)\(^t\bf{\rm{A}}\)という形になります。
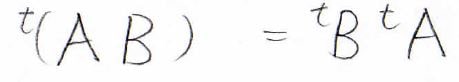
逆行列
最後、逆行列というものについて紹介します。
これは、ある行列\(\bf{\rm{A}}\)に書けるとその積が単位行列になる行列のことで、\(\bf{\rm{A}}^{-1}\)という表記の仕方をして「エーインバース」などと呼びます。
スカラーで言うところの逆数のようなものだと考えて頂ければ結構です。
そして、例えば\(\bf{\rm{B}}\)が\(\bf{\rm{A}}\)の逆行列であった場合は、かける順番を交換することができて、さらにその積が単位行列になります。

交換が可能であることの証明
先ほども言いましたが、このような交換は一般的には成り立ちません。
逆行列との交換が可能であることを証明するためには、このような変形を考えます。
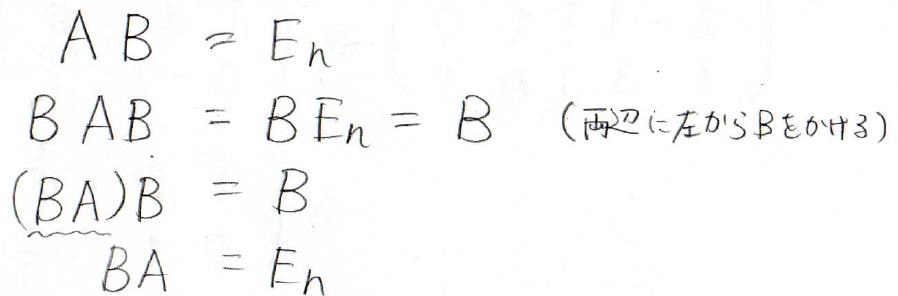
まず、逆行列\(\bf{\rm{B}}\)との積が単位行列になるという式の両辺に左から\(\bf{\rm{B}}\)をかけます。
すると、右辺は\(\bf{\rm{B}}\)になるのですが、左辺を見てみると\((\bf{\rm{BA}})\bf{\rm{B}}\)とみなすことができ、それがまた\(\bf{\rm{B}}\)と等しいということなので、結局\(\bf{\rm{BA}}\)も単位行列であるということになります。
また、この証明には別の方法もあって、\(\bf{\rm{AB}}\)は単位行列ですが、単位行列は\(1\)のようなものなので、単位行列×単位行列と考えることもできます。
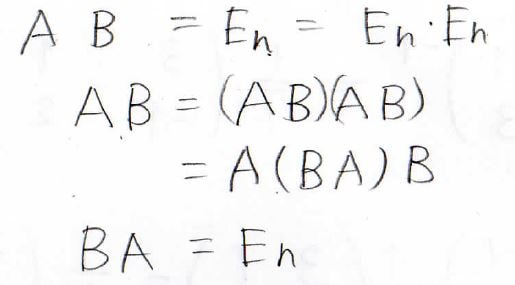
つまり、\(\bf{\rm{AB}}\)は\(\bf{\rm{AB}}\)\((\bf{\rm{AB}})\)になります。
そしてこの関係により、真ん中の\(\bf{\rm{BA}}\)が単位行列であることがわかります。
逆行列の求め方
逆行列を求め方についてお話しします。
まず、何度も出てきている\(\bf{\rm{AA}}^{-1}=\bf{\rm{E}}\)\(_n\)という式の両辺に\(\bf{\rm{A}}^{-1}\)をかけるとこの形になります。
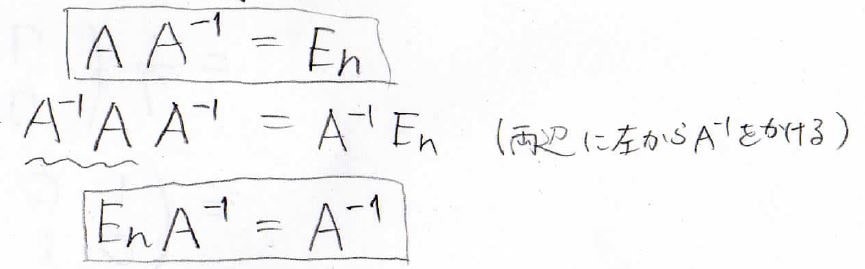
ここで、四角で囲ったこの2つの式を見てほしいのですが、どちらも未知の行列\(\bf{\rm{A}}^{-1}\)に何らかの行列を左からかけて、別の行列になりましたという式になっています。
この形は前回やった連立方程式の解き方で、未知の縦ベクトルだった部分が未知の行列になった形だとみることができます。
詳しくはこちらの記事をご覧ください。

つまりは、逆行列も連立方程式同様に簡約化によって求めることができるようになります。
実際のやり方は、\(\bf{\rm{A}}\)と単位行列を繋げた行列を簡約化して、左側が単位行列となったときに右側に残る行列こそが\(\bf{\rm{A}}^{-1}\)になります。
仮に\(\bf{\rm{A}}\)のランクがその次数より小さい場合には、この操作ができませんが、そのときには逆行列は存在しないことになります。
最もわかりやすい例で言うと、零行列がそうなのですが、すべての行列に逆行列が存在しているわけではないので、覚えておいてください。
練習問題
では最後、練習問題として以下の行列の逆行列を求めてみましょう。

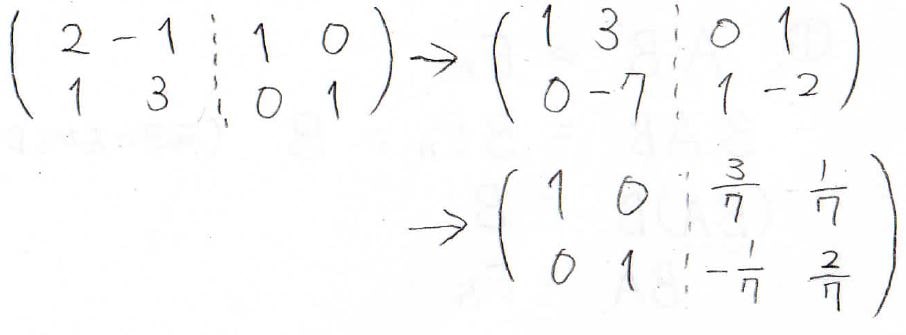
そして、これを簡約化すると右側の行列は、下のような行列になりました。
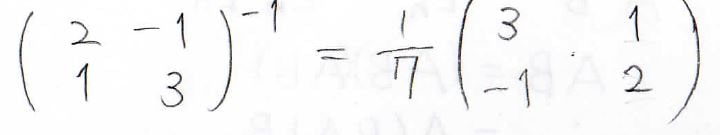
本当にこれが逆行列になっているのか実際に確かめてみると、実際に積として単位行列が得られます。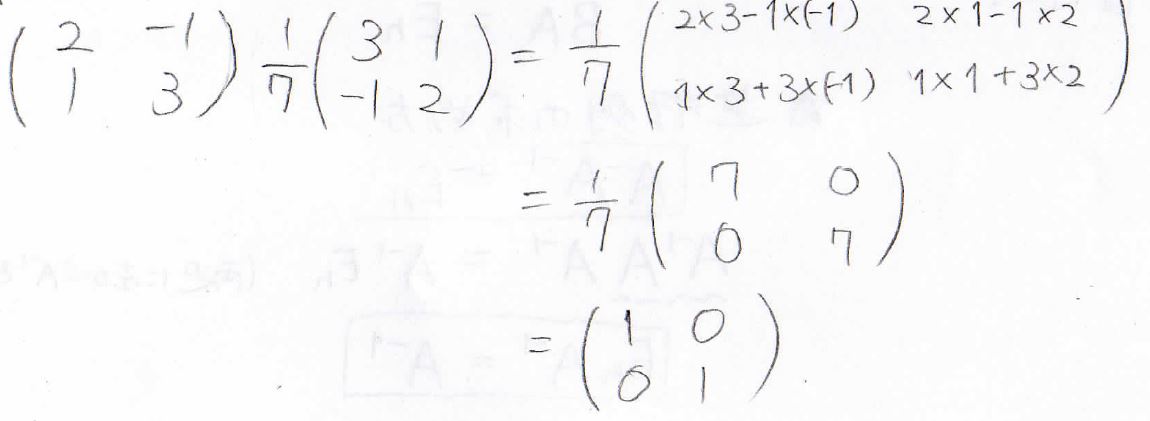
実は、2次正方行列の逆行列は、下のような式で得られるということが知られています。
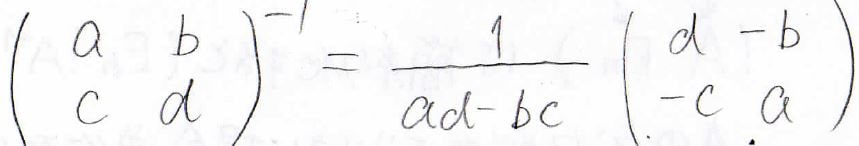
簡約化の手間が省けるので、2次のときくらいは覚えておくのがよいと思います。
ちなみに、分母に\(ad-bc\)とありますが、ここが\(0\)になる場合には行列式が定義できないことになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!



