こんにちは！
今回は、行列の記事第二弾ということで、こちらのテーマでお話ししていきます。
動画はこちら↓
動画で使ったシートはこちら(matrix calculation)
では参りましょう！
行列の足し算
まず、行列の足し算なのですが、これはとても簡単です。
行と列の数が全く同じ行列同士でしか足し算を定義できないのですが、その場合には同じ場所にある成分同士をそれぞれ足したものが和の行列になります。
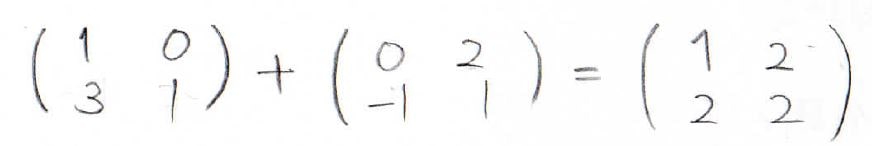
行列の掛け算
続いて掛け算はちょっと複雑なのですが、まず二つの行列をかけるとき左側の行列の列の数と右側の行列の行の数が同じときにしか定義することができません。
そして掛け算ができるときには、左側と右側の行列の各成分をそれぞれ\(a_{ij}\)、\(b_{ij}\)、掛け算の答えとなる行列の各成分を\(c_{ij}\)で表すと、\(c_{ij}\)は\(a_{il}\)×\(b_{lj}\)を\(l\)が\(1\)から\(k\)まで足したものになります。
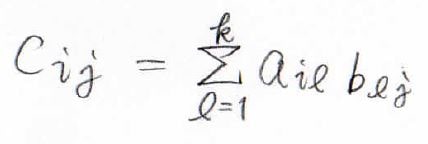
実際に例を見たほうが早いので、例えばこの行列の掛け算を見てみましょう。
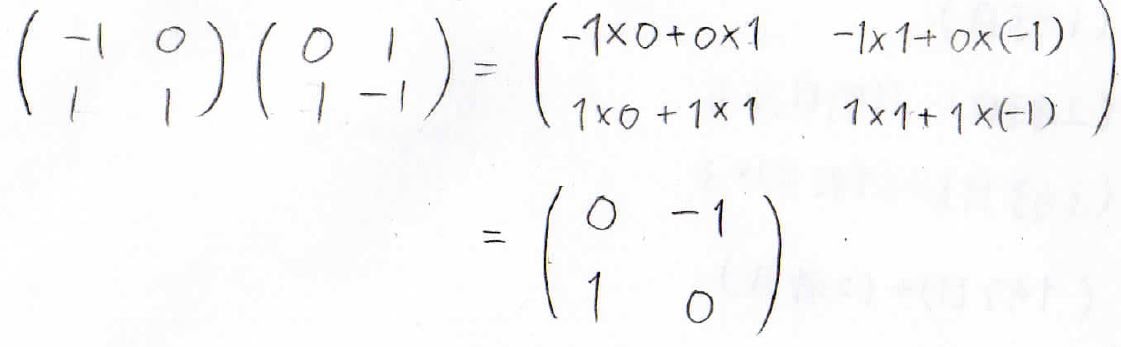
まず、\((1,1)\)成分を考えるときには左側の行列の1行目と右側の行列の1列目に着目します。
そして各行列の\((1,1)\)成分同士をかけて、\(-1\times 0\)が出てきます。
これにもう1つ左側の\((1,2)\)成分と右側の\((2,1)\)成分の積、つまり\(0\times 1\)を足します。
結局\(0+0\)なので、答えの\((1,1)\)成分は\(0\)になります。
\((1,2)\)成分を求めるときには、左側の行列の1行目と右側の行列の2列目に着目して、同じことをやります。
\((2,1)\)成分を求めるときは、左側の行列の2行目と右側の行列の1列目、\((2,2)\)成分を求めるときには、左側の行列の2行目と右側の行列の2列目について同じことをやります。
それでこのようにして行列の積は求められるのですが、行列ではなく縦ベクトルを列が1個の行列としてみなすと、行列とベクトルの積も考えることができます。
例えばこの掛け算では、下のような計算により\((7, -3)\)という縦ベクトルが得られます。
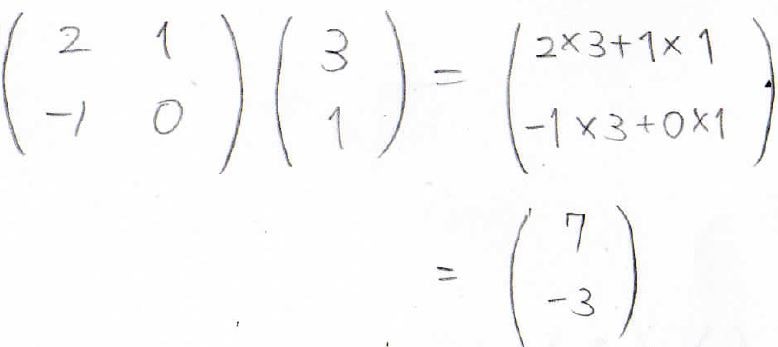
このようにある行列に右から縦ベクトルをかけた場合には、その積は縦ベクトルで与えられることになります。
連立方程式への利用
これの考え方を使うと、実は連立方程式の表記を変えることができます。
これら3つの式の左辺を(ある行列)\(\times (x, y, z)\)という縦ベクトルの積であると考えます。
そしてそれぞれの式の右辺がその答えになるという形です。
この係数だけを取り出した行列のことは、係数行列と呼びます。
ここで、以前の記事でやった簡約化という操作を思い出してほしいのですが、この操作ではかけて足してを繰り返すことで、なるべく簡単な形に変形しようということをやっていました。
詳しくはこちらをご覧ください。
このかけて足してという操作、実は連立方程式を解く操作も全く一緒です。
簡約化ができたときには\(x\)、\(y\)、\(z\)がそれぞれ求まっているということになります。
これを確かめるために、まずは拡大係数行列というものを導入します。
係数行列との違いは、最後の列に右辺が引っ付いていることだけです。
連立方程式は、この拡大係数行列の簡約化によって解くことができます。
そして、例えば係数行列のランクが方程式の数と等しい場合は、簡約化によって係数行列は単位行列にすることができ、このときの一番右側の列が\((x, y, z)\)になっています。
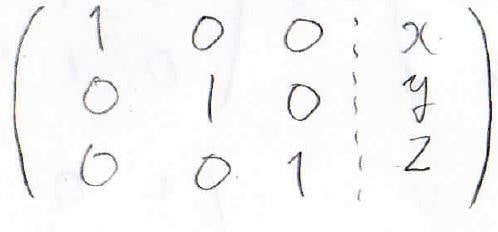
逆に係数行列のランクが方程式の数より小さい場合には、厳密な解を求めることができず、任意の定数を含んだ一般解が得られます。
一般的に「3個の未知定数を厳密に求めるためには3つの条件式が必要になる」ということはよく知られていて、それは正しいのですが、その逆の命題、すなわち「条件式が3つあれば、未知数が3つわかる」というのは成り立ちません。
3つ条件式があり、かつ係数行列のランクが\(3\)であることが未知定数3つが厳密に求まるための十分条件になります。
練習問題
では最後、練習問題としてこの2つの連立方程式を解いてみましょう。
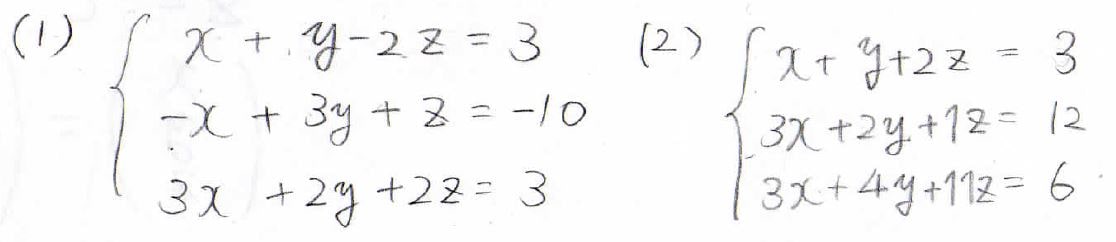
行列を使わなくても、中学校からやっているやり方でも解くことはできますが、せっかくですから簡約化を使って解いてみましょう。
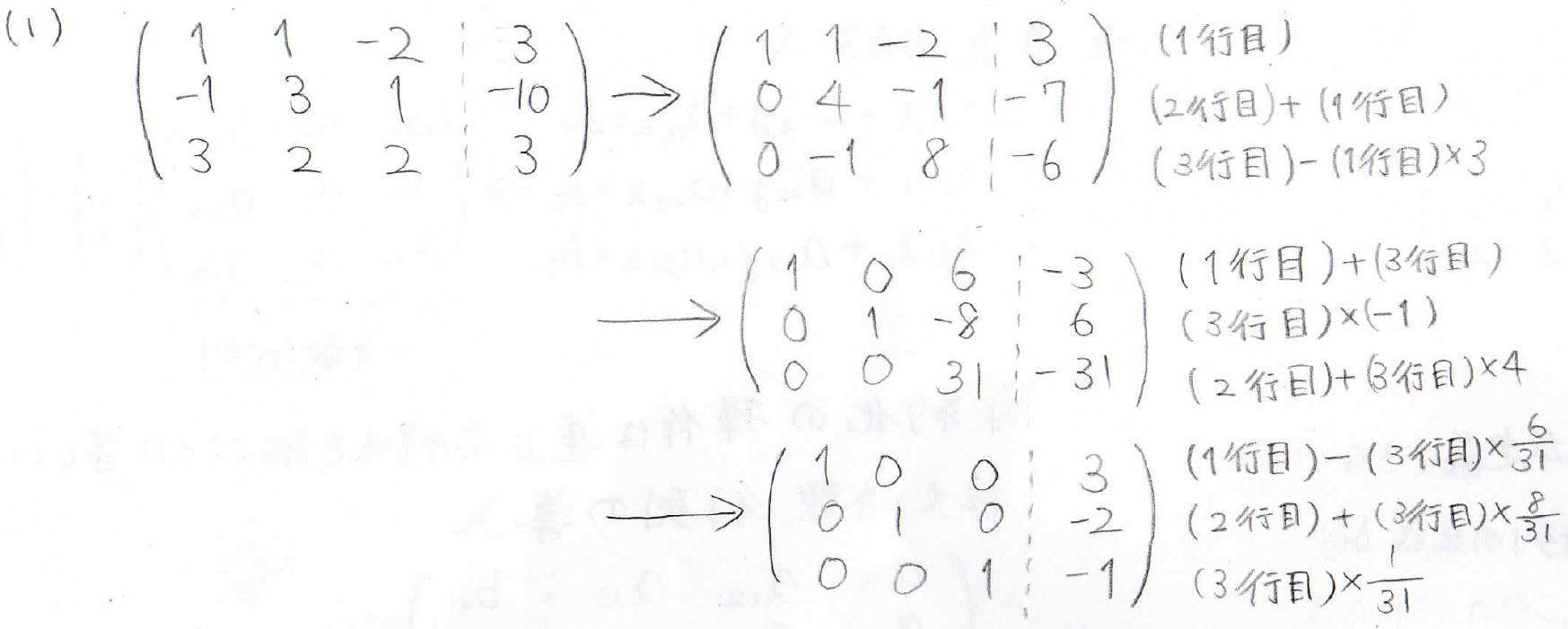
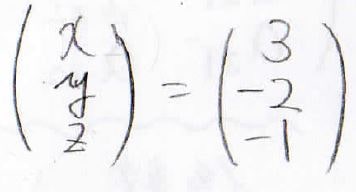
4列目がそのまま、\((x, y, z)\)になるので、解は\((x, y, z)=(3, -2, -1)\)となります。
(2)でも同様に拡大係数行列を作って簡約化します。
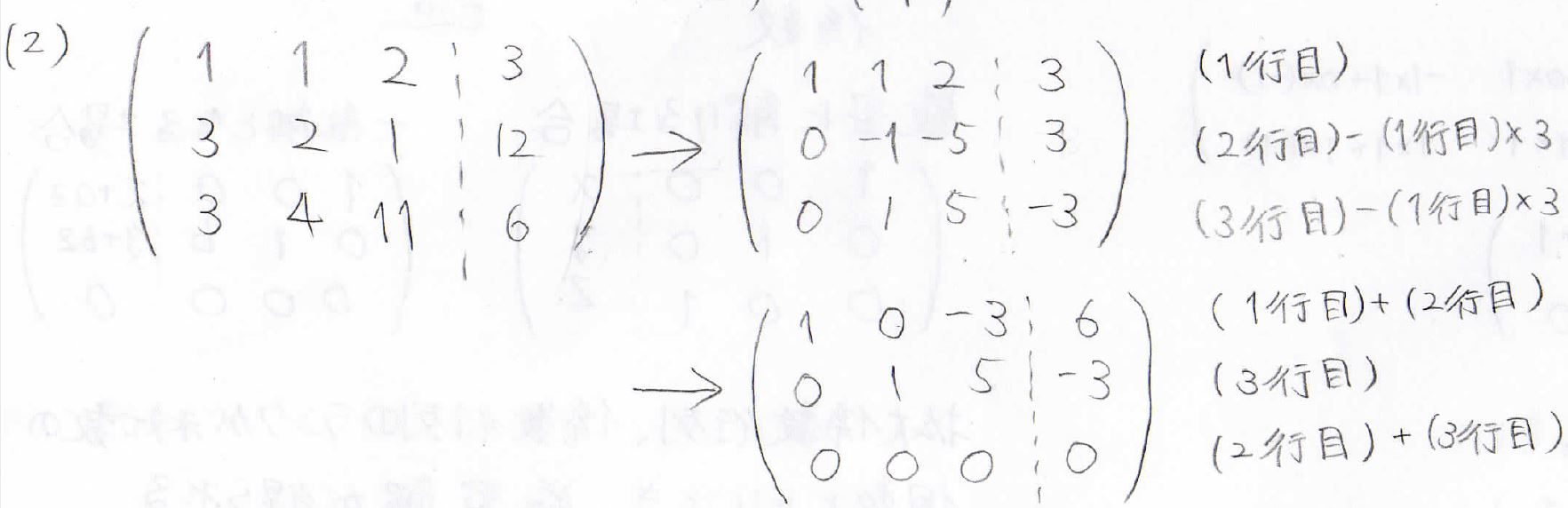
するとこの通りランクが\(2\)でした。
この場合は、3つのうちどれか1つを任意の定数としておくことで一般解が得られます。
仮に\(z\)を任意の定数\(C\)とした場合、\((x, y, z)=(6+3C, -3-5C, C)\)となります。
これには、例えば\((6, 3, 0)\)や\((3, 2, -1)\)といった解が含まれます。
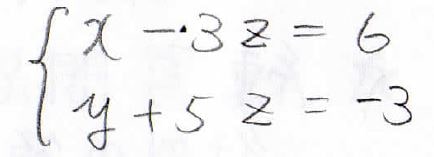
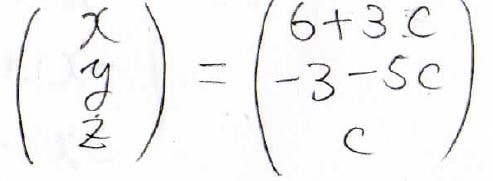
まとめ
という事で今回は行列の加法乗法と連立方程式についてお話ししました。
重要な部分をおさらいしておくと、まず、行列同士の足し算では、同じ行と列の成分同士を足したものが答えの成分となりました。
掛け算は少し複雑で、左側の行列の\(i\)行目と右側の行列の\(j\)列目に着目してその内積を取ったものが答えの\((i,j)\)成分となります。
行列と縦ベクトルの積は縦ベクトルになるので、これを使うと連立方程式を行列とベクトルで表現することができます。
係数を取り出した行列は係数行列、方程式の右辺も含めた行列を拡大係数行列と言って、その簡約化により連立方程式を解くことができます。
ただし、厳密な解を得られるのは係数行列のランクが未知定数の個数と同じになった場合のみで、ランクが小さい場合は足りない数だけ任意の定数を入れて、一般解という形で方程式を解くことができます。
それではどうもありがとうございました！
