こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
すでにやった原子価結合法に関しては、こちらの記事をご覧ください。

動画はこちら↓
動画で使ったシートはこちら(mo)
分子軌道法の考え方
まず、MO法における波動関数の考え方を見ていきます。
MO法では、1個の電子は2個の核によって拘束されていると考えます。
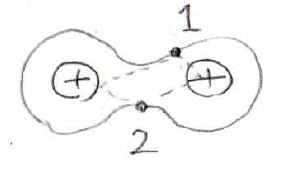
つまり、水素分子イオンのポテンシャルに拘束された電子が2個存在しているということです。
これら2つの波動関数の積が全体の波動関数だと考えます。
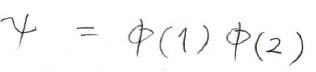
水素分子イオンの波動関数は、以前の記事で求めたとおりです。
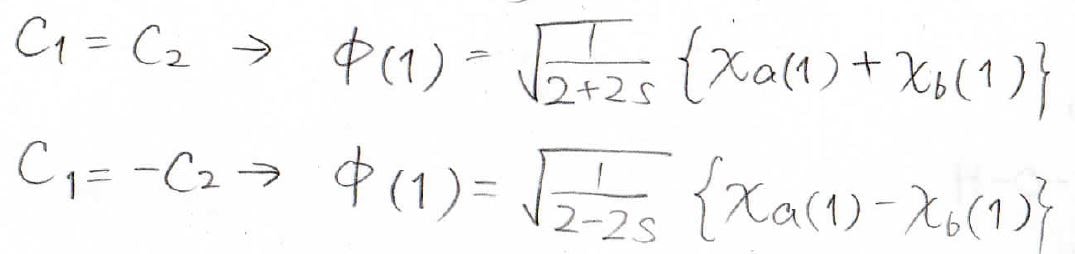
詳しくはこちらの記事をご覧ください。
水素分子の基底状態のエネルギーを計算
先ほどの波動関数を使って、水素分子の基底状態のエネルギーを求めてみます。
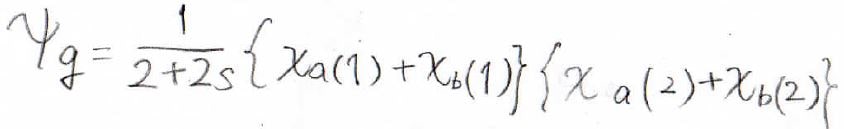
簡単のため、ハミルトニアンを下のように書き換えておきます。

\(1\)の電子の運動に関連するものを\(H_1\)、\(2\)の電子に関連するものを\(H_2\)と表します。
エネルギーは、下のように書けます。
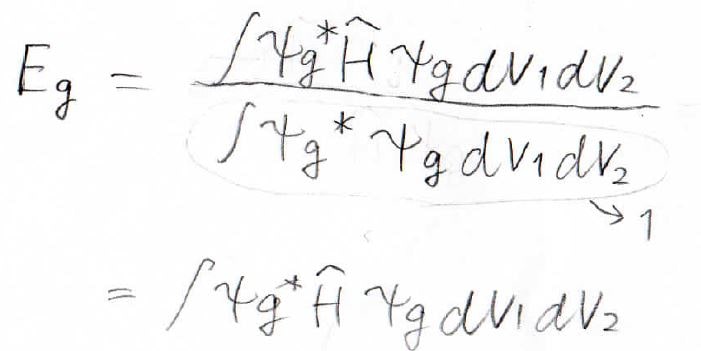
そして、このように変形していきます。
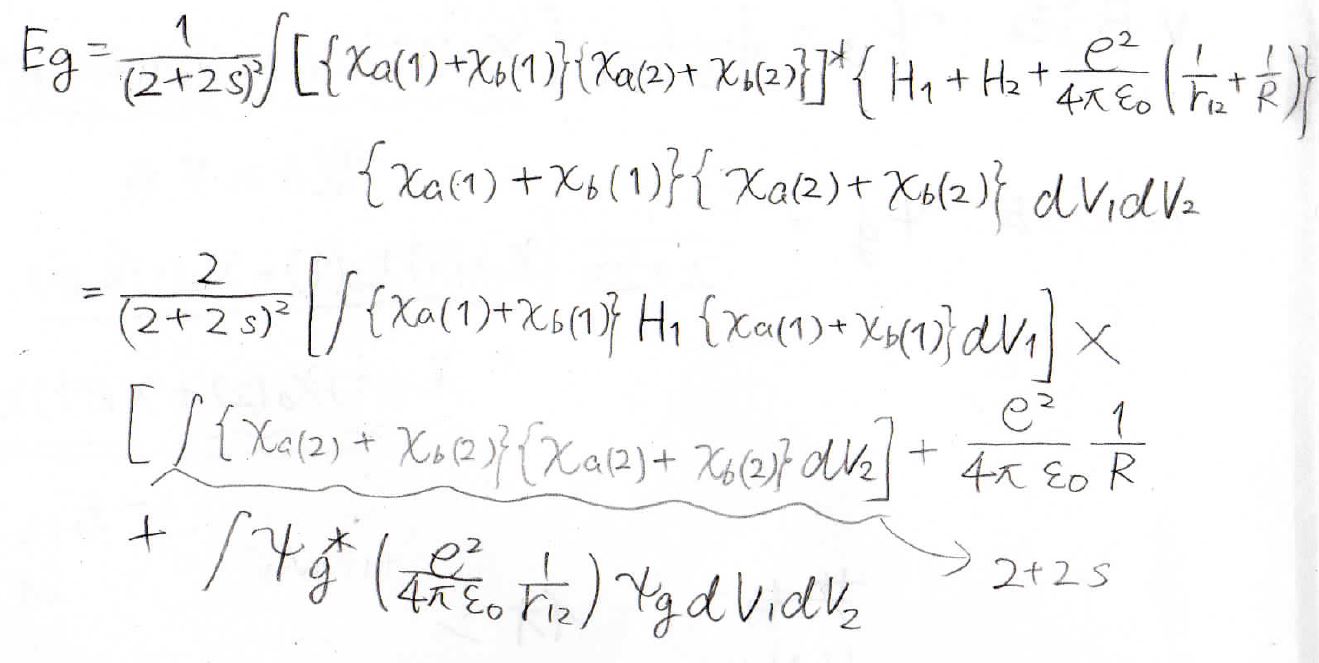
最終的に得られたのが、こちらの式です。
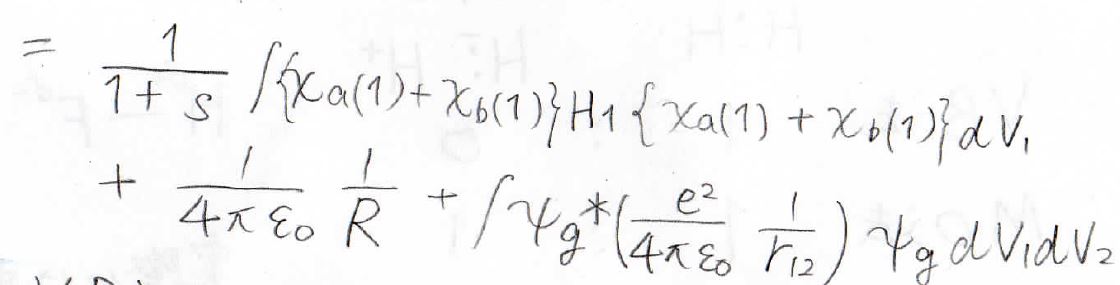
VB法、実験との比較
ここからは、以上の結果が実際の水素分子の結合エネルギーをどれだけ説明しているのか見ていきます。
まず、核間距離\(\displaystyle R\)に対して、結合性軌道のポテンシャルカーブはすべて非調和振動子のものになります。
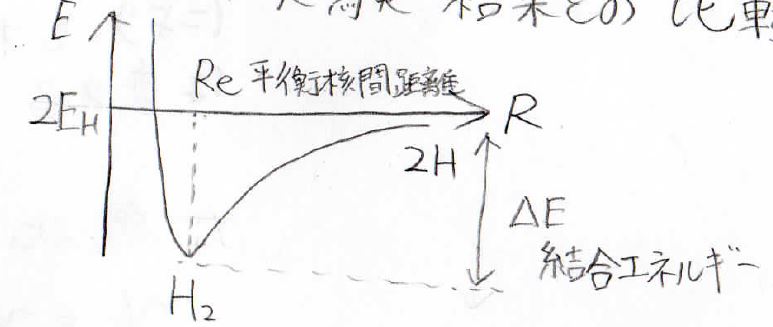
MO法、VB法、実験から求めた結合エネルギーは、それぞれ下記の値になります。

ここで、\(R_\rm{e}\)がポテンシャルが極小をとる平衡核間距離、単位が\(\unicode{x212B}\)(オングストローム)、すなわち\(10^{-10}\ \rm{m}\)です。
結合エネルギーの単位は、\(\rm{eV}\)(エレクトロンボルト)です。
この2つのモデルにはいずれも実験値と無視できないほどの差があって、そこまで精度よく水素分子を再現できるものではないということがわかります。
より現実に近い考え方
これの理由を考えるために、改めてVB法とMO法の波動関数を見てみましょう。
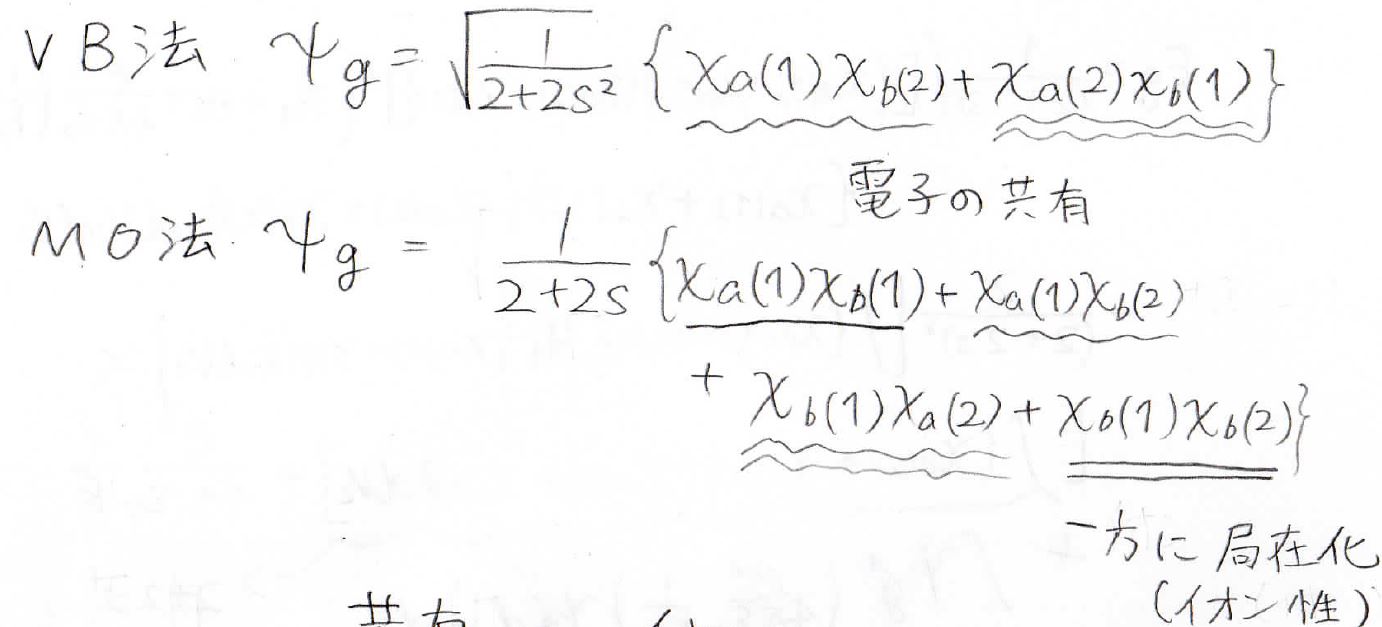
すると、VB法では1つの核につき1個の電子を拘束しているのに対し、MO法では2個の電子が一方の核に拘束されている、すなわちイオン的になっている項が入っています。
したがって、VB法では電子の共有のみを考えており、MO法では電子の共有結合とイオン結合が1:1の比で効いていることになります。

しかし、実際にある結合では、電気陰性度の差や共鳴効果によって、どれだけイオン結合的になっているのかは変わります。
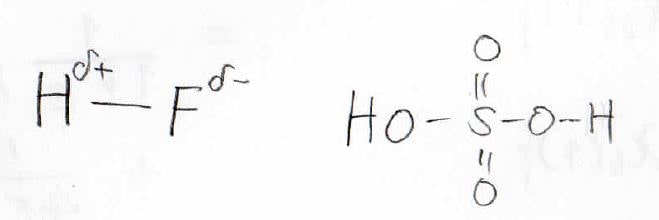
そのため、それぞれの寄与が1:1としか考えられないMO法では、実験結果を精度良く予想することができません。
そこで、より一般化されたモデルとして、この比を自由に変えられるようにしたものが出てきました。
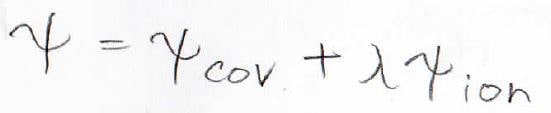
定数である\(\lambda\)に\(0\)から\(1\)までの数値を入れることで、共有結合とイオン結合の比を自由に変えられるようになります。
実際の値は、電気陰性度などの物理パラメータと変分定理を使って求めることになります。
共有結合とイオン結合は、はっきりと分けられるわけではなく、現実の化学結合は、それらの中間にあるイメージです。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!