こんにちは!
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(polar coordinates)
では早速行きましょう!
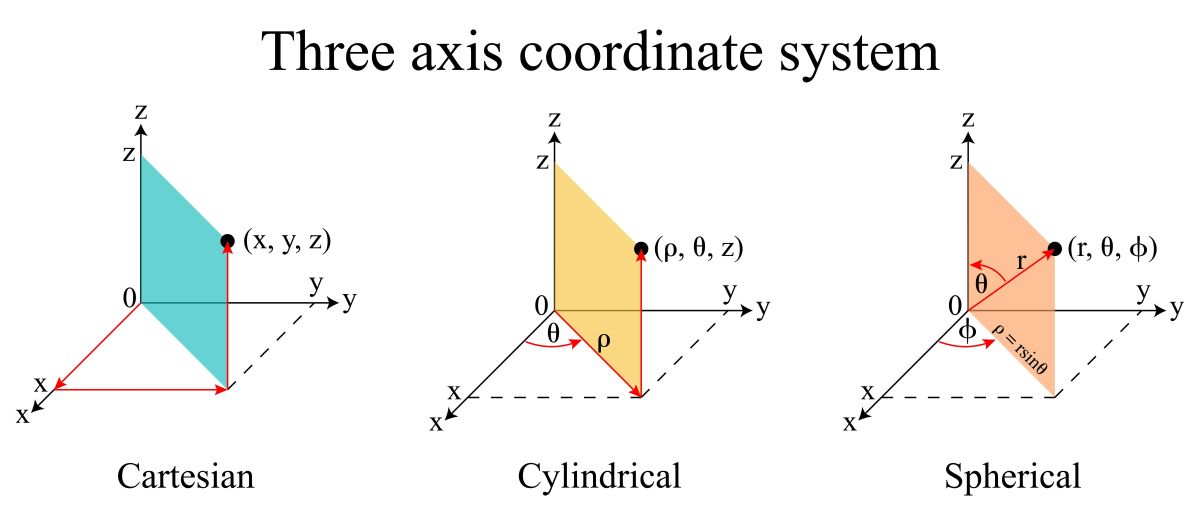
座標の表し方
座標という言葉は、中学校で習うと思いますが、ある空間の中の特定の位置を示す言葉です。
座標は、いくつかの独立なパラメータの組み合わせで表現され、そのパラメータの数が次元数となります。
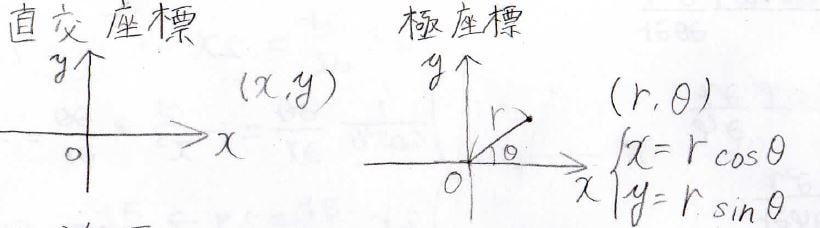
二次元の座標の表し方としてすぐに思いつくのは、\(x\)軸と\(y\)軸が直角に交わっているものだと思いますが、極座標でも独立に変化させられるパラメータは2つです。
\(x\)と\(y\)または\(r\)と\(\theta\)を決めれば、平面上の任意の点を指定することができます。
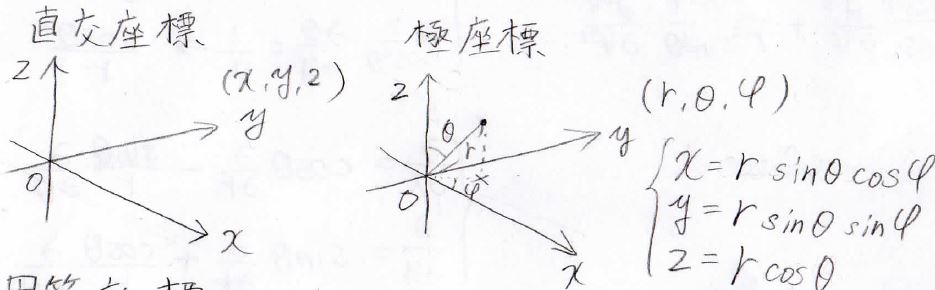
三次元の場合も直交座標、極座標があります。
三次元の極座標は原点からの距離\(r\)と2つの角度パラメータで表現できます。
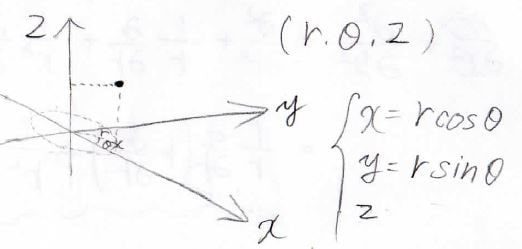
少し変わった形として円筒座標というものもあります。
まず、\(xy\)平面の位置を極座標で指定した後に、\(z\)で高さを表します。
\(\boldsymbol{\nabla} ^2\)の極座標変換
座標の話は以上で、ここからは演算子の座標変換について考えてみたいと思います。
シュレディンガー方程式には、\(\boldsymbol{\nabla} ^2\)が出てきます。
水素原子の電子について計算する場合は、極座標で計算するのが普通ですので、今回はその準備として、極座標での\(\boldsymbol{\nabla} ^2\)の導出を行っていきます。
計算上の注意点
今回示す最終的な結果に至る過程では、下記のように偏微分の順番は入れ替わっても、値は変わらないという前提の操作を行います。
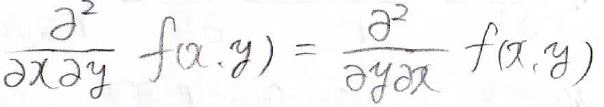
これは、数学的には常に成り立つものではなくて、偏微分する関数が\(C^2\)級である必要があります。
\(C^2\)級というのは、2回偏微分することが可能で、さらに4つすべての2階偏導関数が連続であるということを言います。
そのため、本来この操作を行うためには、この関数が\(C^2\)級であることを確かめないといけない(シュワルツの定理)ですが、自然科学でこれを逐一確認することはほとんどありません。
それは、自然科学の分野で扱う実用的な関数では、偏微分の順序交換が成り立つことがほとんどだからです。
我々は当たり前のように順序交換をしますが、数学的にそれはタブーだということは覚えておいてください。
実際の変形過程
\(x\)、\(y\)、\(z\)を極座標で、また逆に\(r\)、\(\theta\)、\(\varphi\)を直交座標で表すと下のとおりになります。
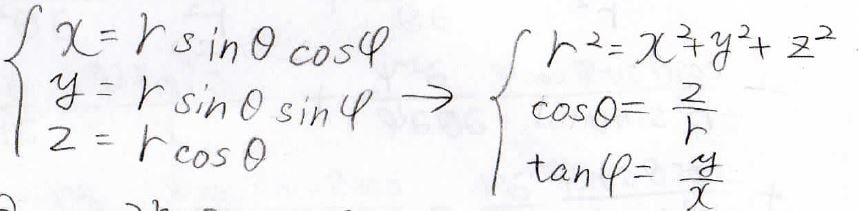
\(\displaystyle \frac{\partial }{\partial x}\)は\(r\)、\(\theta\)、\(\varphi\)を使って下の形になるので、波線を引いた部分を\(x\)、\(y\)、\(z\)が入らない形にすれば、完全に極座標に変換できます。
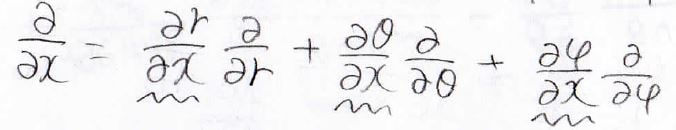
始めに、\(\displaystyle \frac{\partial r}{\partial x}\)を考えてみると、\(r^2=x^2+y^2+z^2\)より、下の式が得られます。
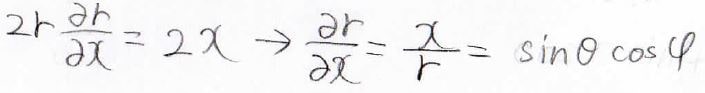
そこから、\(\displaystyle \frac{\partial r}{\partial x}=\frac{x}{r}\)ということになり、これを極座標で表すと\(\sin{\theta}\cos{\varphi}\)となります。
同様に、\(\displaystyle \theta\)、\(\displaystyle \varphi\)についても、以下のようになります。

これを\(y\)と\(z\)についてもやった結果、下のようになります。
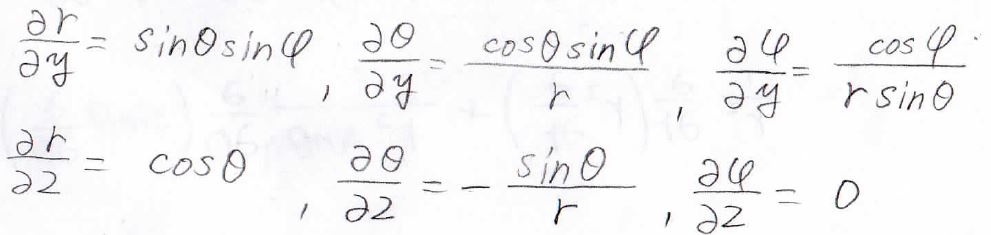
この結果より、\(\displaystyle \frac{\partial }{\partial x}\)は次のようになりました。
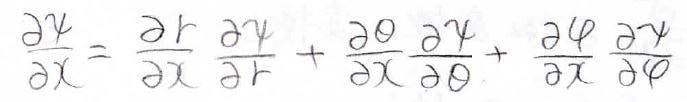
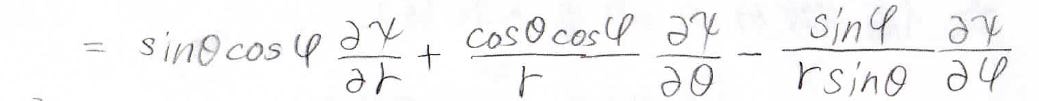
\(\displaystyle \frac{\partial ^2}{\partial x^2}\)を求める場合は、関数の積の微分の公式を使います。
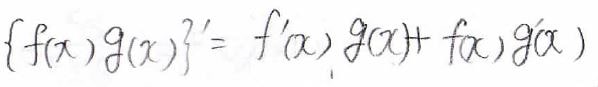
すると、下のようになります。
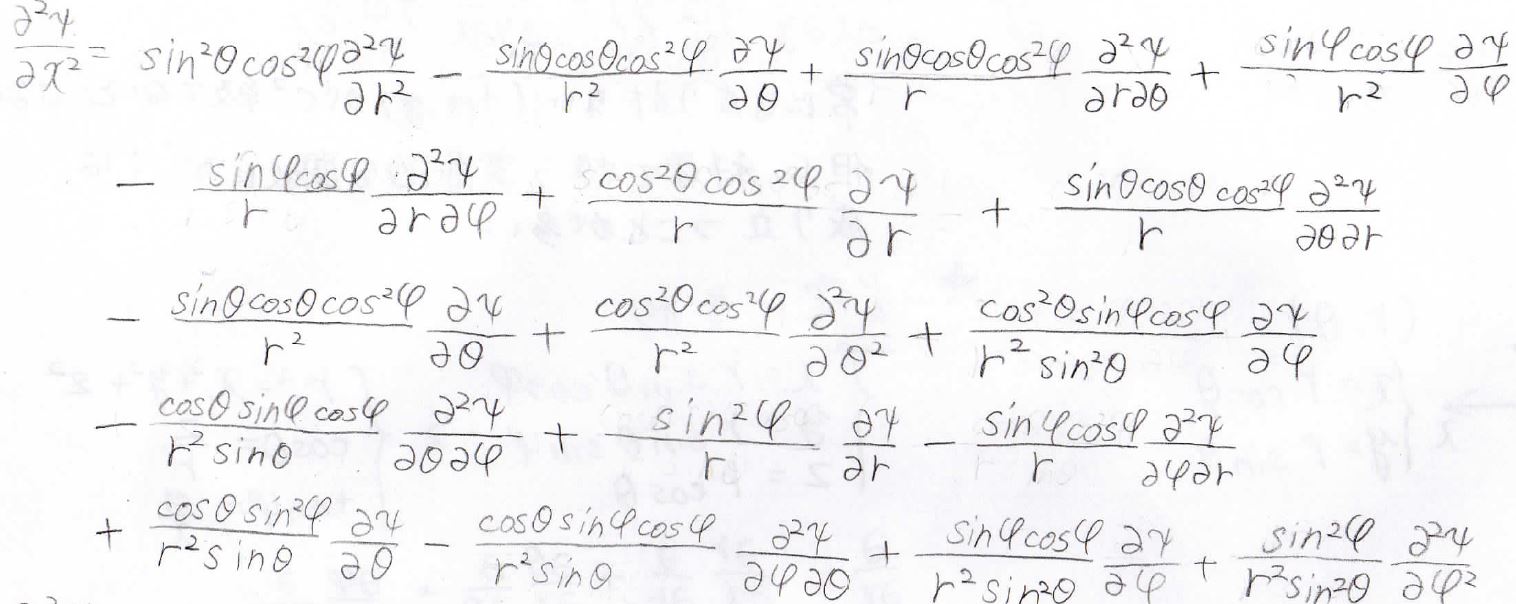
これを\(y\)、\(z\)についてもやってみると、以下のようになります。
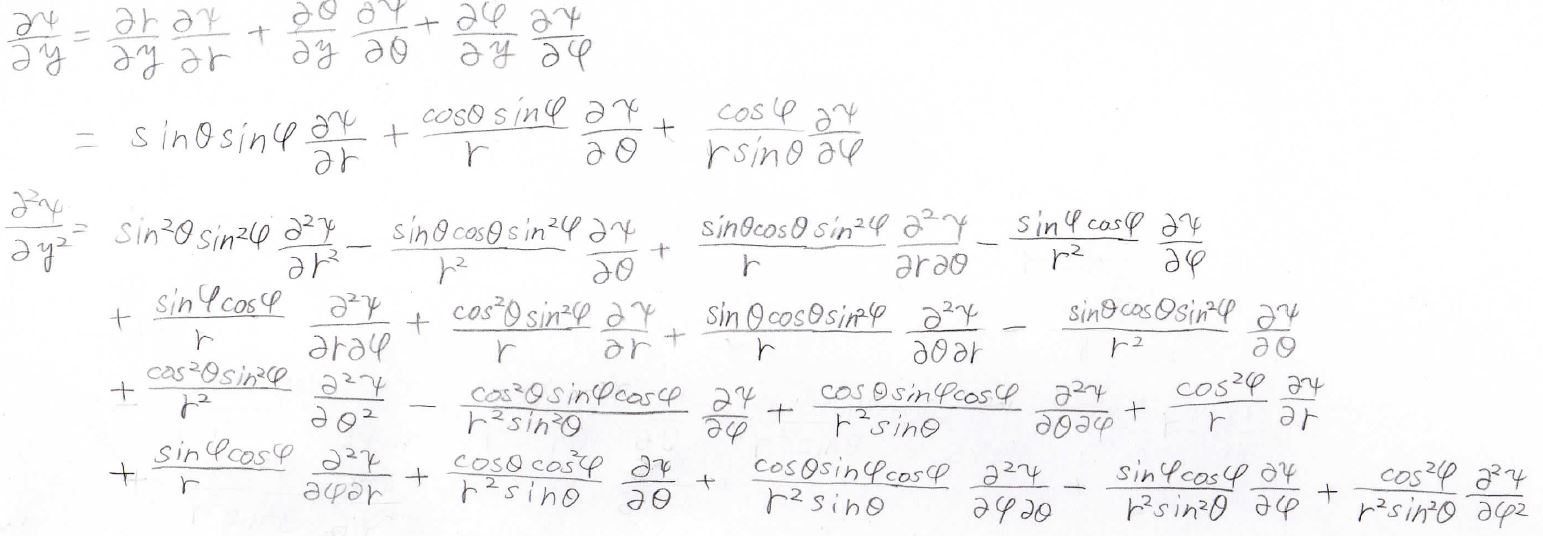
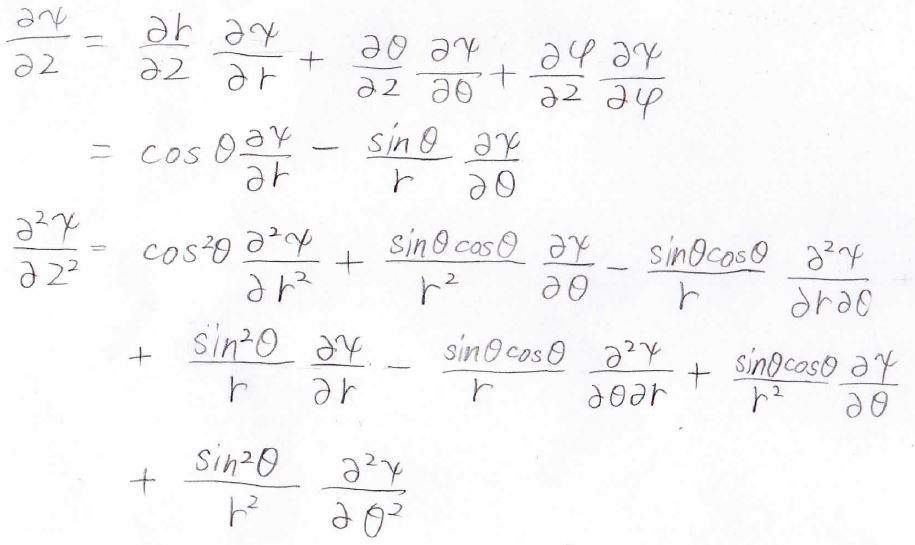
キャンセルする部分がいくつもあり、最終的に得られる\(\boldsymbol{\nabla} ^2\)は次の形になります。
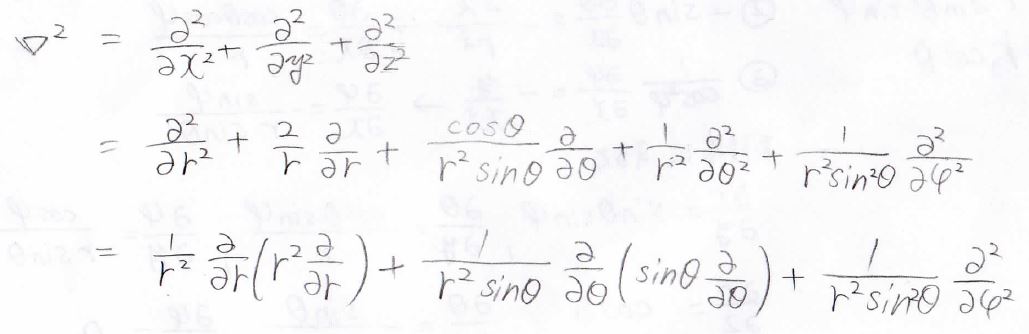
大変な変形なので、わざわざ自分でやってみる必要もないとは思いますが、やり方だけ知っておいてもらえたらと思います。
練習問題
それでは最後、練習問題をやってみましょう。
先ほどは三次元で変形したのですが、二次元の場合はどうなるでしょうか?
\(\displaystyle \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial x^2}\)を\(r\)と\(\theta\)を使って表してみてください。
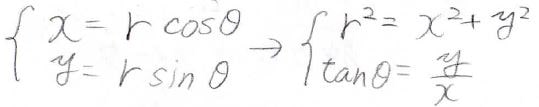

まず、\(\displaystyle \frac{\partial}{\partial x}\)と\(\displaystyle \frac{\partial}{\partial y}\)は、下の形になります。
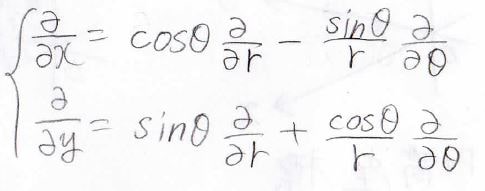
最終的に\(\displaystyle \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial x^2}\)は、このような形となります。
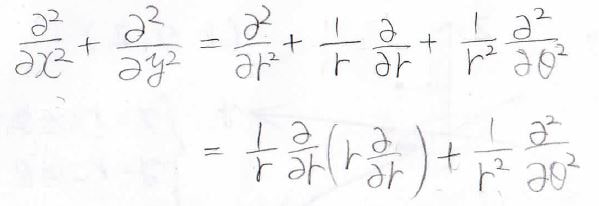
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!