こんにちは！
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(total derivative)
それでは内容に入っていきます！
\(C^n\)-級関数
まずは、\(C^n\)-級関数の定義についてお話ししていきます。
\(x\)と\(y\)について偏微分可能な二変数関数\(f(x,y)\)があったとして、偏導関数\(\frac{\partial f}{\partial x}\)と\(\frac{\partial f}{\partial y}\)がともに連続の時、\(f(x,y)\)は\(C^1\)-級関数であるといいます。
また、2階の偏導関数は全部で↓の4つがありますが、これらが全て連続であるときには、\(f\)は\(C^2\)-級となります。
もっと一般的には、\(n\)次偏導関数が全て連続の時、\(f\)は\(C^n\)-級関数であるといいます。
さらに、無限回偏微分可能であり、高次偏導関数もすべて連続である場合は、\(f\)は\(C^\infty\)-級関数であるといいます。
偏微分の順番入れ替えは可能か？
はい、それでは続いて、偏微分の順番入れ替えについてお話ししていきます。
例えば2次偏導関数の中には、\(y\)について偏微分してから\(x\)で偏微分する場合と\(x\)について偏微分してから\(y\)で偏微分する場合があります。
\(x\)と\(y\)の順番が入れ替わった時に、その値が変わらないのかということですが、この入れ替えは一般的には成り立ちません。
つまり、常に可能という訳ではありません。
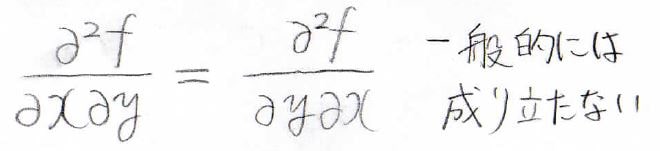
ただし、\(f\)が\(C^2\)-級であった場合には、この入れ替えが可能になります。
これをシュワルツの定理といいます。
ここでは割愛させていただきますが、平均値の定理より証明ができます。
そして、数学をやっている人からすると、ここが受け入れにくいところですが、自然科学で扱う関数では、この入れ替えが可能な場合が多いです。
そのため、特に偏導関数の連続を確かめることなく、偏微分の入れ替えをすることがほとんどです。
数学的には、必要な段階を踏んでいるわけではないので、これから自然科学をやろうとしている場合には、ここをしっかり押さえておいてほしいと思います。
全微分
それでは、全微分の話に移っていきます。
全微分可能であることの定義は次のとおりです。
\(f(x,y)\)が点\((a,b)\)で全微分可能であるというのは、\(f(x,y)\)は\((a,b)\)で連続であり、\(C(a,b)=0\)となる連続関数\(C(x,y)\)を使って、点\((a,b)\)の周辺で\(f(x,y)=f(a,b)+A(a-x)+B(y-b)+\rho (x,y)C(x,y)\)という形で\(f(x,y)\)が表せる、というものです。
ここで\(A\)と\(B\)は定数であり、\(\rho (x,y)\)は点\((x,y)\)と点\((a,b)\)の距離になります。
もし、点\((a,b)\)から点\((a+dx,b+dy)\)まで、ほんの少しだけ動いたことを考えると、\(f\)の変化量\(\rm{d}\)\(f=A\rm{d}\)\(x+B\rm{d}\)\(y+\sqrt{\rm{d}\mathit{x}^2+\rm{d}\mathit{y}^2}\rm{d}\)\(C\)となります。
右辺の第三項は\(dx\)と\(dy\)がとても小さい場合はほとんど\(0\)になるため、無視した場合には、\(\rm{d}\)\(f=(\frac{\partial f}{\partial x})_y\rm{d}\)\(x+(\frac{\partial f}{\partial y})_x\rm{d}\)\(y\)となります。
\(\rm{d}\)\(f\)をこのようにして表したものを\(f\)の全微分と呼びます。
熱力学では、この全微分が頻繁に出てきますので、ぜひここで押さえておいてください。
練習問題
それでは、最後ちょっとした頭の体操をやってみましょう。
\(\rm{d}\)\(f=a\rm{d}\)\(x-b\rm{d}\)\(y\)のとき、\(\frac{\partial b}{\partial x}\)を\(a\)と\(y\)を使って表すとどうなるでしょうか。
ただし、\(f\)は\(C^2\)-級であるとします。
となります。
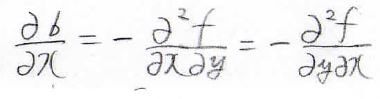
\(a\)は\(\frac{\partial f}{\partial x}\)なので、これを代入することで、\(\frac{\partial b}{\partial x}=-\frac{\partial a}{\partial y}\)となります。
まとめ
それでは今回の内容は以上なので、最後軽くおさらいをやって終わります。
今回は全微分をテーマにお話ししました。
\(n\)次偏導関数がすべて連続である関数のことを\(C^n\)-級関数、無限回偏微分可能であり、高次の偏導関数もすべて連続な関数のことを\(C^\infty\)-級関数と呼びます。
そして\(n\)次偏導関数において、偏微分の順番入れ替えは、\(f\)が\(C^n\)-級であるときに可能になります。
しかし、自然科学では、この交換ができることが多いため、特に連続であるとかは確かめずに、交換されることが多いです。
これから自然科学をやろうという人は、常にこの交換ができるわけではないということは抑えておいてください。
それで、全微分可能であることの定義はお話ししたとおりで、一次式で微小変化量を表した形を全微分と呼びます。
この全微分は、熱力学で頻繁に出てくるので、ぜひここで押さえておきましょう。
それではどうもありがとうございました！
