こんにちは!
今回も化学のお話やっていきます。
今日のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(well potential)
じゃあ、さっそく内容に入っていきましょう!
量子の不確定性
以前、シュレディンガー方程式の導出を行った記事でも触れた、電子の二重スリット実験の話をします。
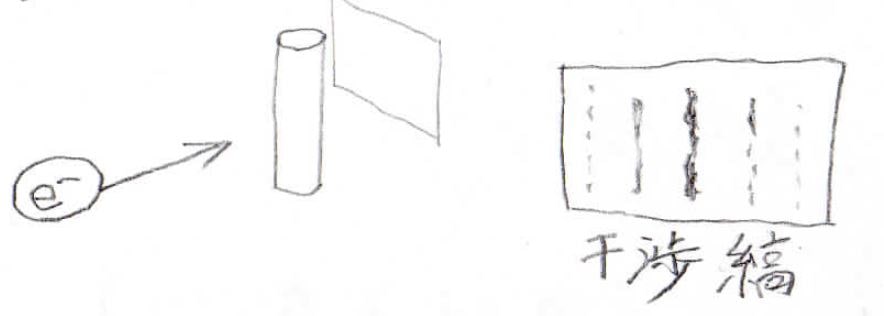
電子は波の性質をもっていることで、自身と干渉した後、スクリーンのどこかに粒子として衝突します。
その後も電子を1個ずつ打ち出していくと、スクリーン上には干渉縞が見えてきます。
波として考えれば、干渉縞を作るのはごく自然なことですが、粒子として考えるならば、毎回同じように飛び出した電子が各々別の位置に到達することはありえません。
このように1個1個の運動を完全に予測できないというのが量子の不確定性という性質です。
確率波
しかし、もう一度スリット実験を思い出してみると、確実に言えることがあります。
それは高次の明線ほど、電子は到達しにくく、低次の明線に到達する確率が高いということです。
このことより、この位置に何%の確率で存在しているということは言えそうです。
そこで、確率を表す波の関数で量子の位置を考えることが提案されました。
確率を表す波のことは確率波と呼びます。
シュレディンガー方程式で扱う波動関数\(\varphi\)は複素数ですが、存在確率は\(0\)から\(1\)までの実数になるはずです。
シュレディンガー方程式から電子の存在確率を計算することができるように、\(\varphi\)の大きさの二乗が存在確率にあたるというモデル設定をすることにします。
すると、例えば一次元で\(x_1\)から\(x_2\)までの範囲に電子が存在する確率は、次のように表すことができます。
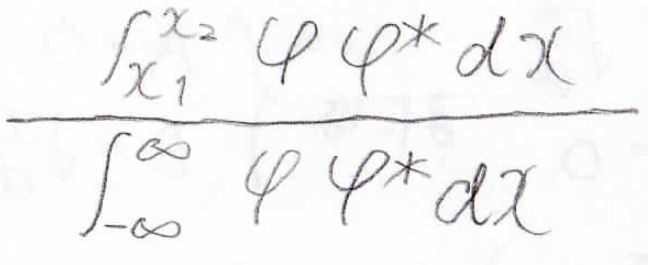
確率は\(\displaystyle 0\)から\(\displaystyle 1\)までの値になるはずなので、規格化するためにこの値で割っています。
グラフで表すと、斜線部の面積が電子の存在確率になります。

この確率波の考え方は、提唱された当時、あのアインシュタインにも認められず、なんとシュレディンガーさえも否定的でした。
しかし、実際の現象との整合性が多く確かめられる結果となり、今では受け入れられています。
一次元井戸型ポテンシャル
では実際に、波動関数を使って、実際に電子のエネルギーを求めてみましょう。
最も計算が簡単な系は、今回紹介する一次元井戸型ポテンシャルモデルです。
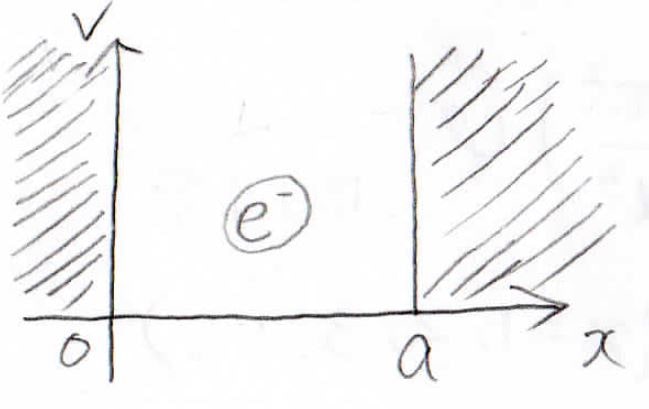
ある一次元の領域\((0,a)\)の区間に、電子が1個存在していたとします。
この区間のポテンシャルエネルギーは\(0\)とします。
また、ここ以外の領域には電子が絶対に存在しないという意味で、ポテンシャルエネルギーを\(\infty\)とします。
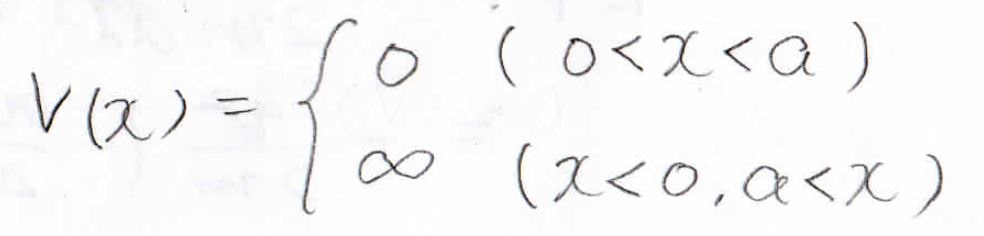
\(x=0, a\)の地点も電子が存在していないので、\(\varphi (0)=\varphi (a)=0\)になります(境界条件)。
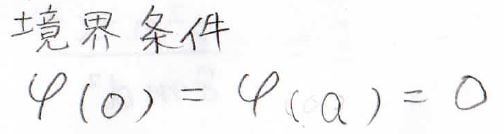
また、\((0,a)\)の範囲に必ず電子があるので、存在確率\(|\varphi (x)|^2\)の定積分が\(1\)になるという条件をあらかじめ立てておきます(規格化条件)。
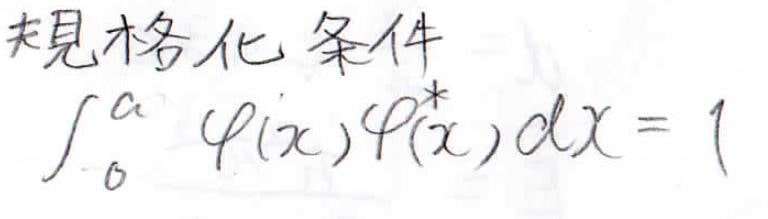
\((0, a)\)までの範囲におけるシュレディンガー方程式は、ポテンシャルが\(0\)なので、下のような形になります。
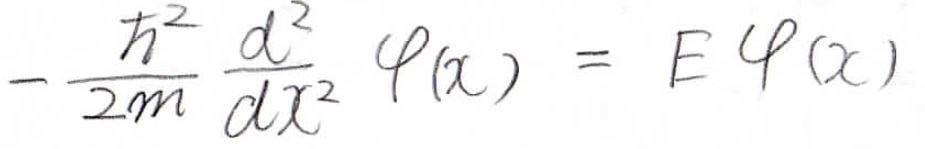
これは単純な微分方程式であり、特性方程式はこのようになります。
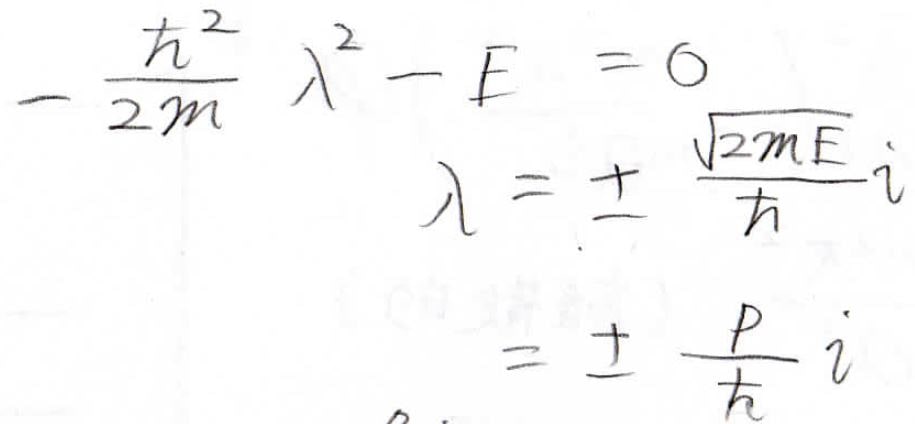
さらに、エネルギー\(E\)と運動量\(p\)は、\(\displaystyle E=\frac{p^2}{2m}\)の関係になるので、\(\displaystyle \lambda=\pm \frac{p\rm{i}}{\hbar}\)となります。
したがって、波動関数はこのようになります。
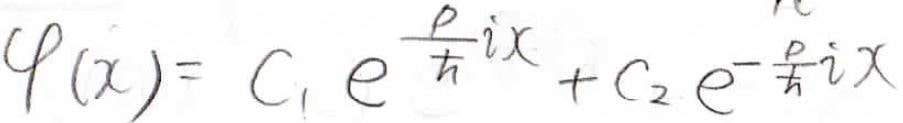
次に、オイラーの公式を使って、この波動関数を変形すると、この形になります。
ここで\(\varphi (0)=0\)という境界条件があったので、それを当てはめると\(C_1+C_2=0\)となるので、\(\varphi (x)\)は\(\sin\)だけで表せるということになります。

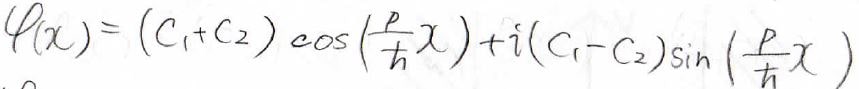
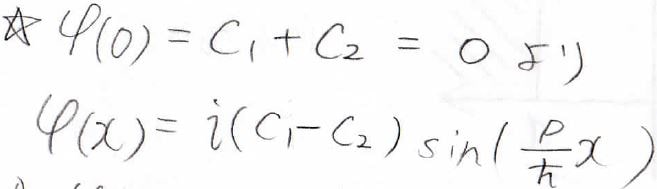
また、\(\varphi (a)=0\)であることから、\(\displaystyle \frac{p}{\hbar}=\frac{n\pi}{a}\)となります。
ただし、\(n\)は自然数です。

続いて、係数部分\(\rm{i}(C_1-C_2)\)を\(A\)という複素数で表すことにして、規格化条件よりこの係数を求めてみます。
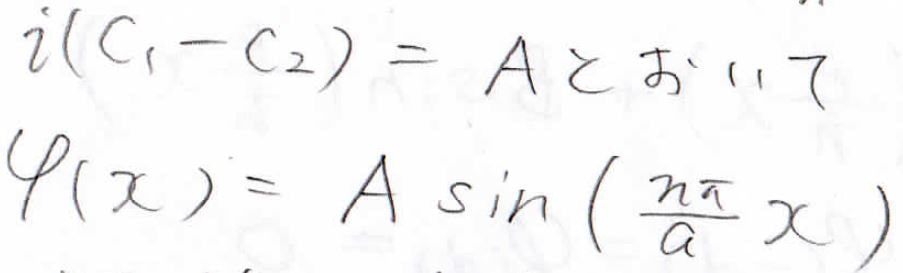
すると、\(\displaystyle \frac{aA^2}{2}=1\)という式が出てきます。
\(A\)は、この条件を満たす複素数であれば何でもいいので、ここでは最も単純に、実数の\(\displaystyle \sqrt{\frac{2}{a}}\)としておきます。
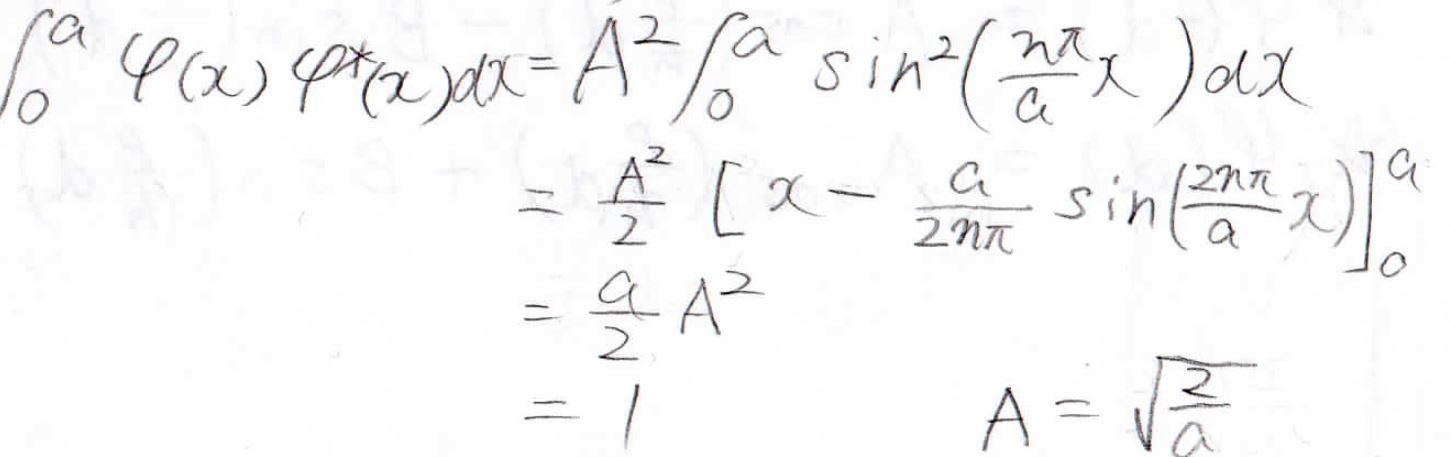
すると、波動関数は下のようになります。

最後に、電子が持つエネルギーを求めてみます。
この計算はかなり簡単で、下記のように計算できます。
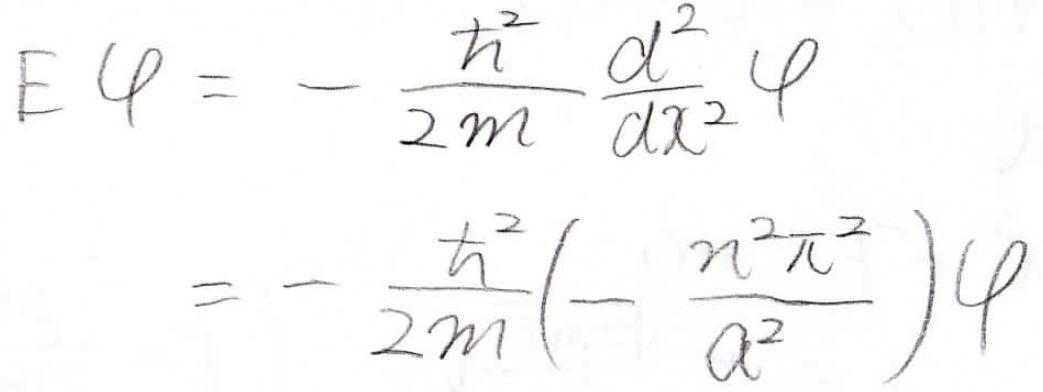
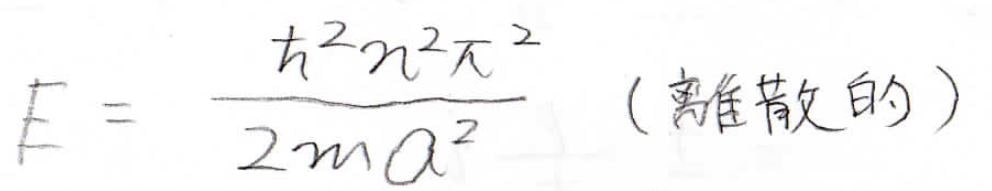
ここで注目してもらいたいことは、量子のエネルギーが不連続な値となるということです。
縦軸をエネルギーとして図で表すと、下のようにになって、このエネルギー準位の間のエネルギーをもつ電子は存在していないということになります。
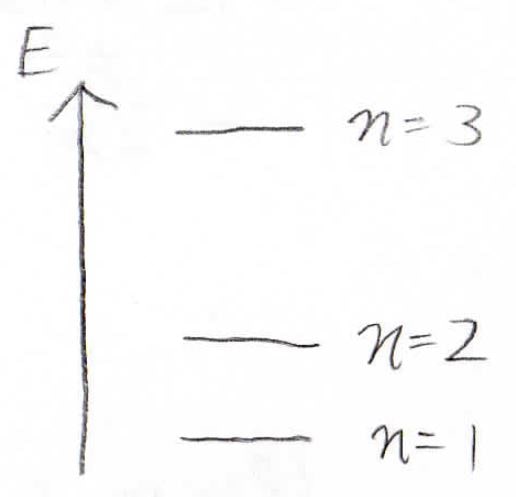
量子のエネルギーは、とびとびの(離散的な)値を持つという性質があるということは、ぜひ知っておいてください。
実は、我々が普段目にしている物に色がついているのは、量子のエネルギーが不連続だからです。
詳しくはこちらで解説しています。

練習問題
最後に、練習問題をやって終わろうと思います。
さっきは\((0, a)\)という範囲でしたが、今度は\((-d, d)\)という範囲に拘束された電子の波動関数とエネルギーを求めてくださいという問題です。
先ほどの条件とは、座標がずれただけなので、もちろんエネルギーは一致するはずです。
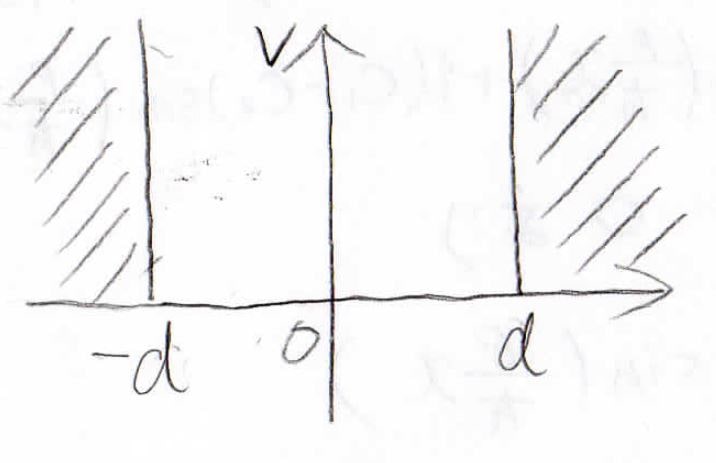

まず、境界条件は\(\varphi (-d)\)と\(\varphi (d)\)が\(0\)になるというものなので、下のような式が得られます。
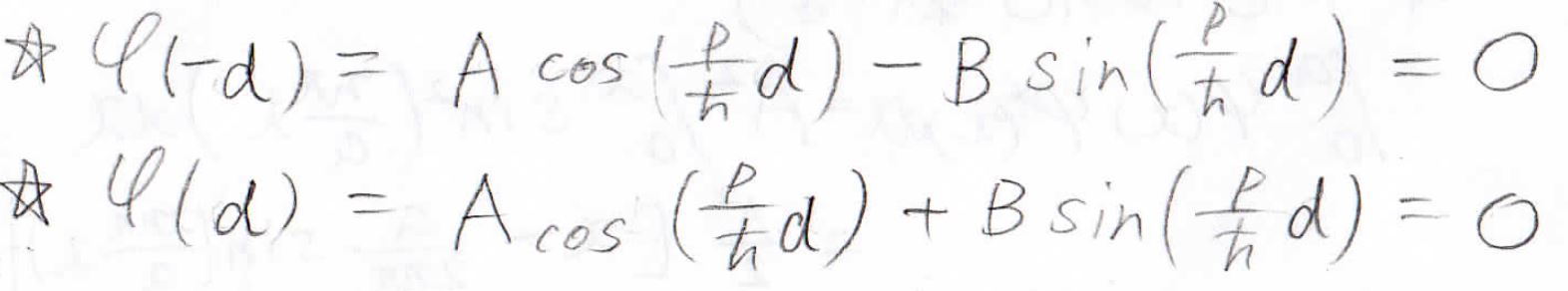
\(A\)と\(B\)が両方\(0\)になればこの式は満たされますが、規格化条件を満たすことができません。
したがって、\(A\)と\(B\)の片方だけが\(0\)として、\(\displaystyle \cos(\frac{pd}{\hbar})\)と\(\displaystyle \sin(\frac{pd}{\hbar})\)のうち、\(0\)ではない係数を持つ方が\(0\)になるということを考えます。
例えば、\(B\)を\(0\)と仮定しましょう。
そのとき、境界条件を満たすためには\(\displaystyle \cos(\frac{pd}{\hbar})=0\)である必要があります。
よって、\(n\)を正の奇数として\(\varphi (x)\)は\(\displaystyle A\cos(\frac{n\pi x}{2d})\)となります。
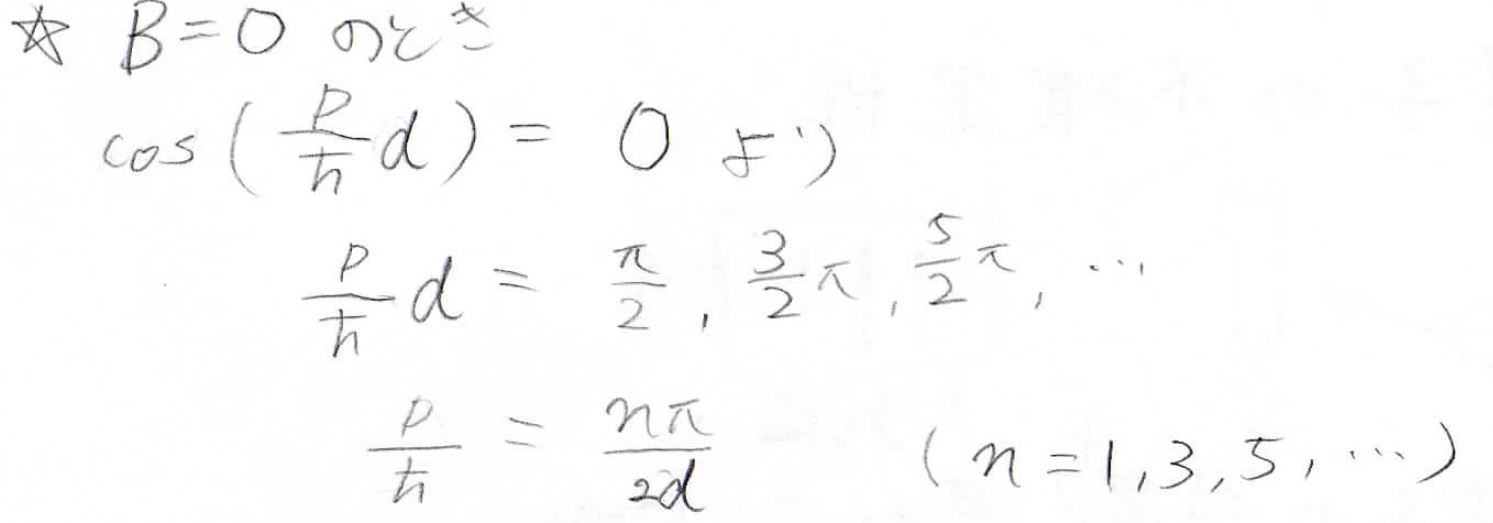
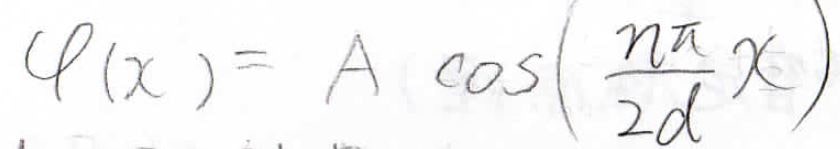
\(A\)が\(0\)のときの\(\varphi (x)\)は、\(n\)を正の偶数として\(\sin\)で書けるということになります。
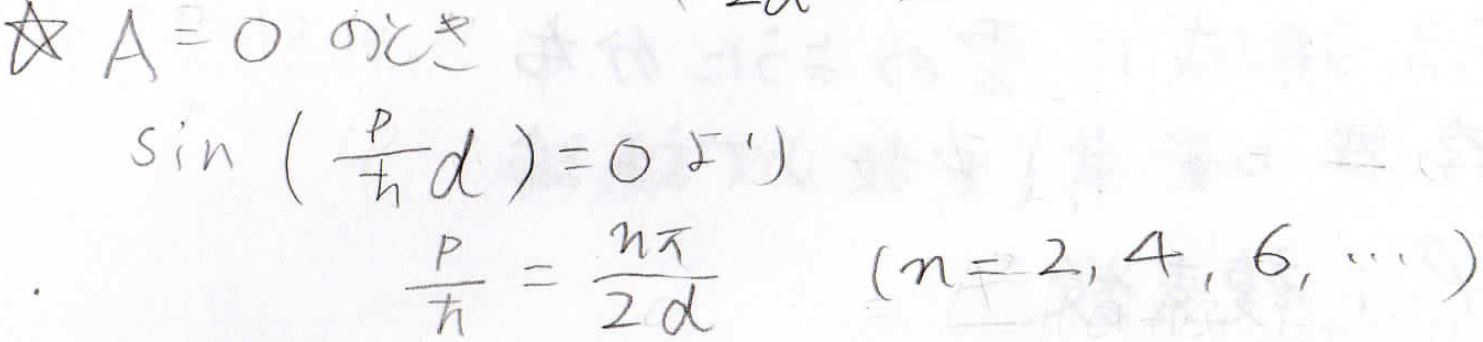
規格化すると、\(0\)でないときの\(A\)と\(B\)は\(\sqrt{\frac{1}{d}}\)となります。
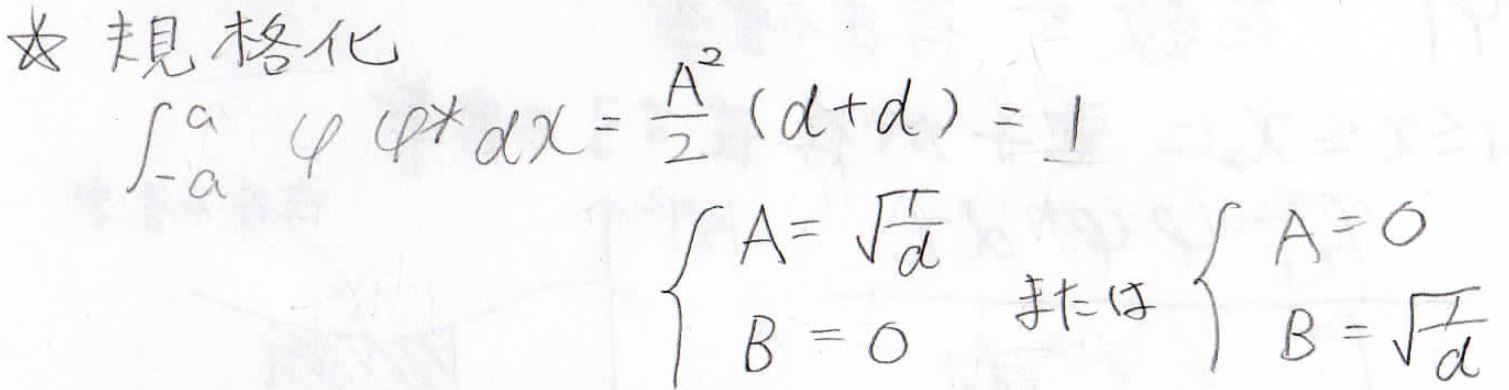
よって\(\varphi (x)\)は、このように\(\sin\)または\(\cos\)という形で表せることになります。
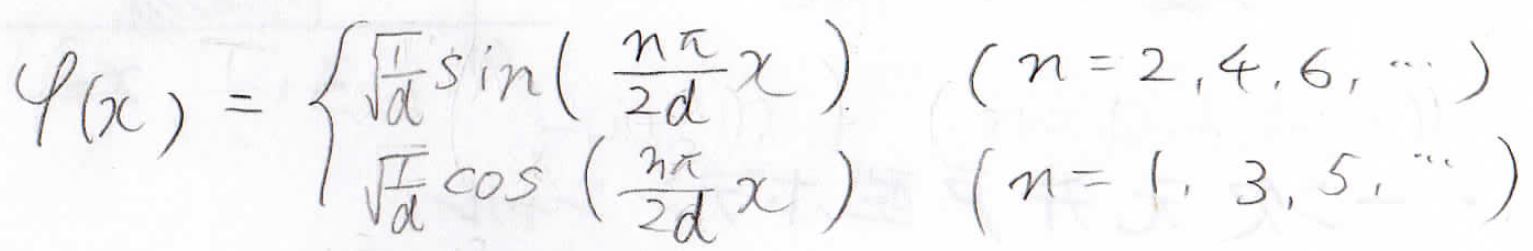
最後にエネルギーを求めると、\(\displaystyle \frac{\hbar ^2n^2\pi ^2}{8md^2}\)となります。
仮に\(d=\displaystyle \frac{a}{2}\)とすると、先ほど求めた\((0, a)\)の領域のときとエネルギーが等しくなります。
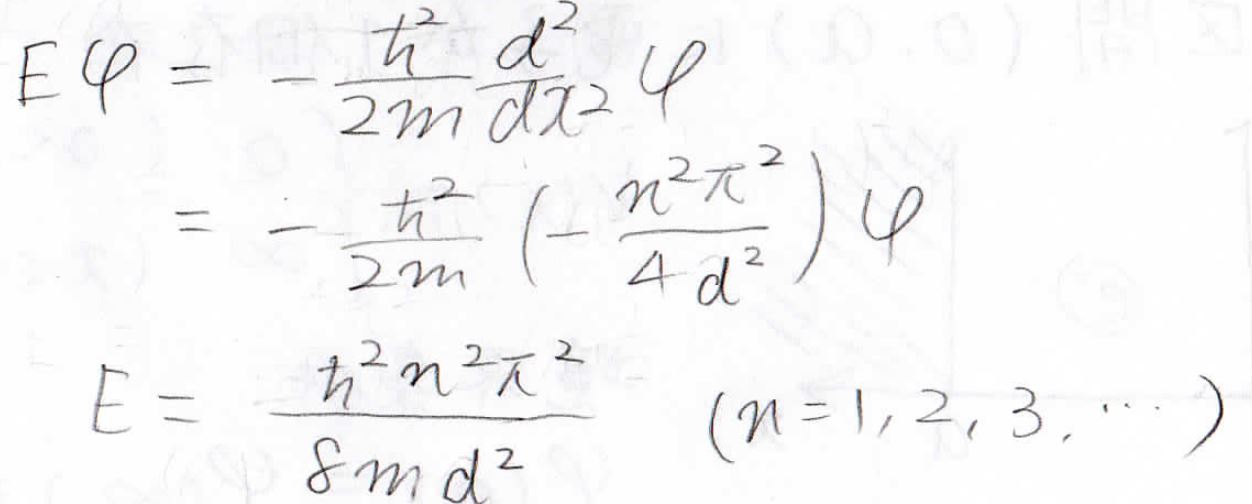

まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!