こんにちは!
今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(approach)
シュレディンガー方程式が厳密に解けないのはどんなときか
水素原子の軌道計算の記事でも触れたのですが、シュレディンガー方程式では、多体問題の解を厳密に求めることができません。
水素原子でも、原子核1個と電子1個という2つの量子があるので、そのままでは解くことができません。
この場合は、ボルン=オッペンハイマー近似によって原子核の動きが止まっていると考えることで、電子1個だけの問題にできるため解くことができて、実験的にもその近似の信頼性が確かめられています。
それでも原子核が2個以上、電子が2個以上の場合は厳密に解くことができないので、いかにしてこれを解くのか、すなわち多体問題をどうやって単体問題に落とし込むのかというのがこの記事の趣旨になります。

近似的に解くための基本的なアプローチ方法
ここでは、基本的なアプローチ方法を2つ紹介します。
摂動法
1つ目は、摂動法というものです。
この方法では、単体問題のハミルトニアンに下のような補正項を入れて計算します。
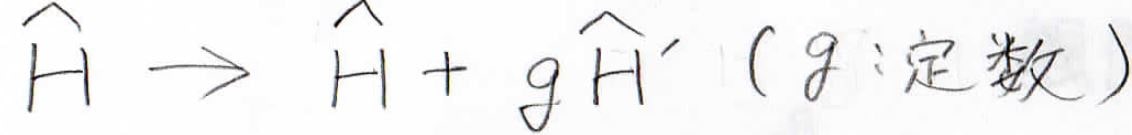
定数である\(\displaystyle g\)は、補正の度合いを表すもので、\(\displaystyle g=0\)は補正前、\(\displaystyle g=1\)は補正後を表します。
そして、波動関数とエネルギーもべき級数で書き換えることで、あらかじめ解ける形にしておきます。
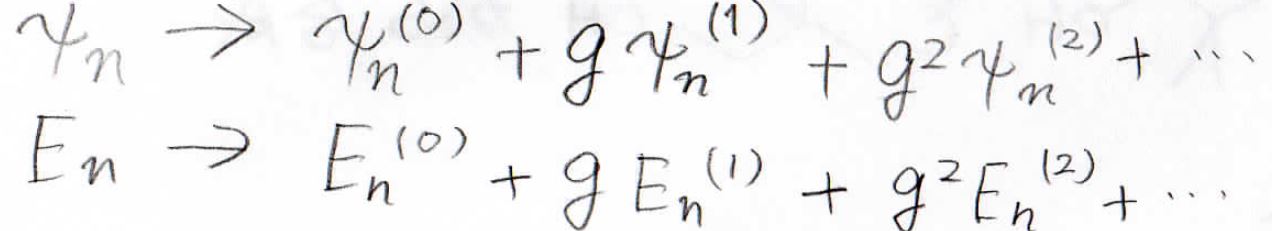
これらをシュレディンガー方程式に当てはめると、両辺が\(\displaystyle g\)の級数になるので、各項の係数が等しくなるための補正項を求めることで、最終的に波動関数とエネルギーを求めることができます。

現実に近いハミルトニアンの補正ができれば、実験結果を予想することができます。
詳細は、こちらの記事をご覧ください。


変分法
もう1つの方法は、変分法と言います。
この方法では、始めに波動関数の形をおおまかに予測します。
ただし、正確に予想できるわけがないので、未知の定数を含む形で波動関数を作ります。
この波動関数のことは、試行関数と呼びます。
ここからエネルギーを求めるために、まずはシュレディンガー方程式の両辺に左から\(\psi ^\ast\)をかけます。

すると、右辺に\(\psi ^2\)、すなわち電子の存在確率が表れるので、全空間についての積分でエネルギーを求めることができます。
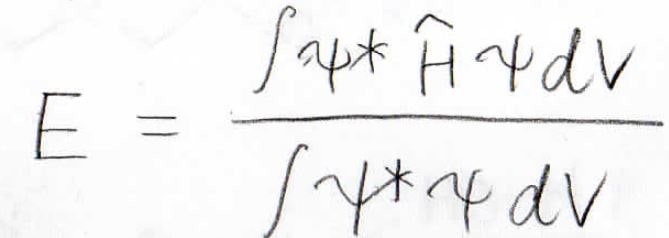
ただし、このエネルギーは未知の定数を含んでいるので、まだ数値的に求められたわけではありません。
実際に観測されるのは、エネルギーが低い状態であるはずなので、エネルギーを未知定数\(C\)について微分して\(0\)になる極値を探します。
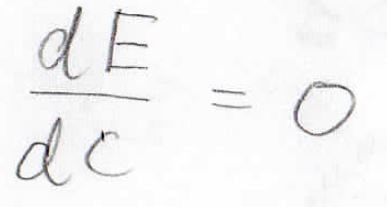
エネルギーが極小となるときの\(C\)が計算できると、波動関数が数値的に求められることになります。
詳細はこちらの記事をご覧ください。


まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




