こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(diffusion limiting reaction)
それでは内容に入っていきます!
気相と液相の反応速度の違い
気相
まず、以前お話しした衝突理論のおさらいから始めます。
衝突理論は、気相の単純な化学種間で起こる化学反応の反応速度定数を予想するものです。
詳しくは、こちらを参照してください。

ここでは結論だけを示しますが、2つの分子間で起こる反応の反応速度定数\(k\)は、2分子の半径の和を直径とする円の面積\(\pi d^2\)と絶対温度の平方根\(\sqrt{T}\)に比例し、分子のモル質量の平方根\(\sqrt{M}\)に反比例します。
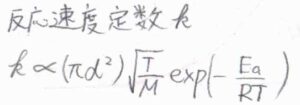
これは、下図における円柱の体積に由来するものです。
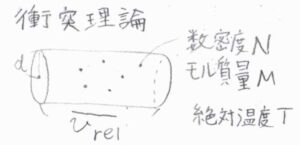
この円柱の中に分子中心があると、単位時間の間にいま着目している分子と衝突が起こります。
そして、反応速度定数が\(\displaystyle \exp{(-\frac{E_\rm{a}}{\mathit{RT}})}\)に比例するというのは、反応に最低限必要なエネルギーの要請を表します。
衝突が起こった分子のうち、一定以上のエネルギーに達しないものとは、反応が起こらないことを示しています。
液相
一方、溶液中で起こる反応の場合は、気相に比べて分子間距離がきわめて短いため、分子間相互作用を無視することができなくなります。
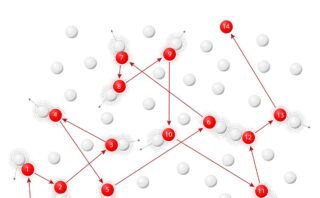
ある分子が位置を変えるためには、周囲の分子を押しのける必要があります。
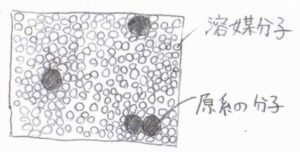
それにより、気相中における反応に比べて、反応系の分子同士の衝突頻度は低下します。
しかしその一方で、一度接近した分子同士が再び離れることも困難となるため、反応系の分子どうしが接近して離れるのにかかる時間は、気相よりも長くなります。
これを籠効果といいます。
分子同士が接近した瞬間にエネルギーが足りなくも、その長い接近時間の間に周囲の分子から、反応に必要なエネルギーを獲得できれば、反応が起こる可能性があります。
籠効果を考慮した反応機構
ここからは、液相中における反応の過程を段階に分けて考えていきます。
ここでは、二成分\(\rm{A}\)と\(\rm{B}\)が1分子ずつ消費されて、生成物\(\rm{P}\)が1分子できる反応を例に考えます。
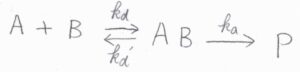
まず反応の一段階目は、\(\rm{A}\)の分子と\(\rm{B}\)の分子が反応できるほど接近して、分子のペア\(\rm{AB}\)ができるというものです。
二段階目で、\(\rm{AB}\)から生成物\(\rm{P}\)ができます。
ただし、\(\rm{AB}\)は\(\rm{P}\)まで反応することなく、\(\rm{A}\)と\(\rm{B}\)に別れることがあります。
反応速度定数は、\(\rm{AB}\)ができる素反応について\(k_\rm{d}\)、\(\rm{AB}\)が解離する素反応について\(k_\rm{d}’\)、\(\rm{AB}\)から\(\rm{P}\)ができる素反応について\(k_\rm{a}\)とします。
定常状態近似を適用すると、中間体である\(\rm{AB}\)のモル濃度[\(\rm{AB}\)]は、\(\displaystyle \frac{k_\rm{d}[\rm{A}][B]}{k_\rm{a}+\mathit{k}_d’}\)となります。
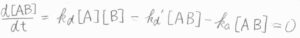
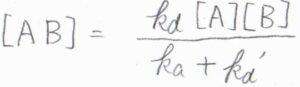
\(\rm{P}\)の生成速度\(\displaystyle \frac{\rm{d}[P]}{\rm{d}\mathit{t}}=k_\rm{a}\)\([\rm{AB]}\)より、\(\displaystyle \frac{\rm{d}[P]}{\rm{d}\mathit{t}}=\frac{k_\rm{a}\mathit{k}_d[A][B]}{k_\rm{a}+\mathit{k}_d’}\)となります。
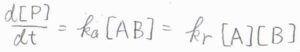
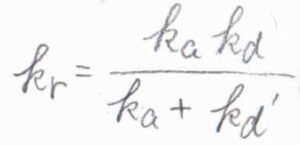
いま、この全体の反応を二次反応として見たときの反応速度定数\(\displaystyle \frac{k_\rm{a}\mathit{k}_d}{k_\rm{a}+\mathit{k}_d’}\)を\(k_\rm{r}\)と表すことにします。
\(k_\rm{d}’\)\(\ll k_\rm{a}\)のとき、すなわち\(\rm{AB}\)の解離よりも、\(\rm{P}\)の生成が速く進行する場合、\(k_\rm{r}\)の分母にある\(k_\rm{d}’\)を無視すると、\(k_\rm{r}\)\( \approx k_\rm{d}\)となります。
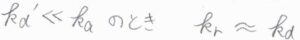
2つの分子が拡散によって接近する過程が、この反応の律速段階となります。
このような反応のことは、拡散律速の反応と呼ばれます。
反対に、\(k_\rm{d}’\)\( \gg k_\rm{a}\)のとき、すなわち\(\rm{AB}\)の解離が速く進行する場合は、\(\rm{A}+B\)と\(\rm{AB}\)の平衡定数を\(K\)として、\(k_\rm{r}\)\( \approx k_\rm{a}\)\( K\)となります。
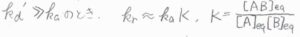
平衡状態にある\(\rm{AB}\)が反応に必要なエネルギーを獲得することで、\(\rm{P}\)へと反応が進行します。
このような反応は、活性化律速の反応と呼ばれます。
前駆平衡の反応速度については、こちらを参照してください。

拡散律速の反応速度定数
ここからは、拡散律速の反応について、拡散方程式を使って考えていきます。
成分\(\rm{A}\)と\(\rm{B}\)が溶けた溶液について、すでに定常状態に達しており、すべての位置について濃度の時間変化\(\displaystyle \frac{\partial c}{\partial t}\)が\(0\)となっていた場合を考えます。
このとき、三次元の拡散方程式より、\(\boldsymbol{\nabla}^2[\rm{B}]=0\)となります。

拡散方程式については、こちらを参照してください。
拡散が等方的に起こったとすると、\(\displaystyle \boldsymbol{\nabla}^2=\frac{\partial^2}{\partial r^2}+\frac{2}{r}(\frac{\partial}{\partial r})\)であるため、\(\displaystyle \frac{\rm{d}^2[B]}{\rm{d} \mathit{r}^2}+\frac{2}{r}\frac{\rm{d}[B]}{\rm{d} \mathit{r}}=0\)という動径についての二階微分方程式が書けます。
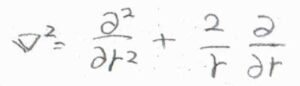
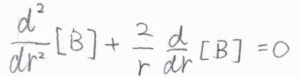
その一般解は、\(C_1\)、\(C_2\)を定数として、\([\rm{B}\)\(\displaystyle ]=C_1+\frac{C_2}{r}\)で与えられます。
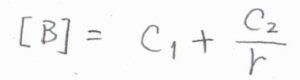
\(C_1\)と\(C_2\)を決定するために、2つの境界条件は、次のように設定します。
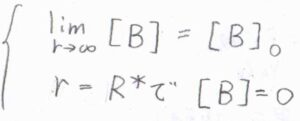
まず、\([\rm{B}]\)の\(r\rightarrow \infty\)の極限は、バルクの濃度\([\rm{B}\)\(]_0\)に収束します。
もう1つの条件は、\(r=R^\ast\)の位置において\([\rm{B}\)\(]=0\)となるというものです。
この条件は、成分\(\rm{A}\)のある1つの分子中心の座標を原点として考えています。
\(R^\ast\)は、反応が起こるために\(\rm{A}\)と\(\rm{B}\)が接近しなければならない距離で、臨界反応距離と言います。
拡散律速の反応では、\(\rm{AB}\)から\(\rm{P}\)への素反応がとても速いので、臨界反応距離において\([\rm{B}\)\(]=0\)と考えます。
これらの条件のもとで、先ほどの微分方程式を解くと、解は\([\rm{B}\)\(\displaystyle ]=(1-\frac{R^\ast}{r})[\rm{B}]_0\)となります。
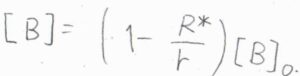
縦軸を\([\rm{B}]\)、横軸を\(r\)としてグラフを書くと、こちらのようになります。

計算上、\(r\lt R^\ast\)の範囲では、\([\rm{B}]\)が負の値となりますが、この範囲では\([\rm{B}]=0\)とします。
ここから反応速度を考えるためには、\(r=R^\ast\)における\(\rm{B}\)の物質量の流束を考えます。
流束を\(J\)とすると、フィックの第一法則より\(J=-D_\rm{B}\)\(\displaystyle (\frac{\rm{d}[B]}{\rm{d}\mathit{r}})_{r=R^\ast}\)と書けるため、\([\rm{B}]\)に微分方程式の解を代入すると、\(\displaystyle J=-\frac{D_\rm{B}[B]}{R^\ast}\)となります。
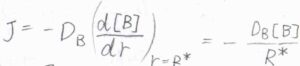
ここで、\(D_\rm{B}\)は\(\rm{B}\)の拡散係数です。
流束の定義、フィックの第一法則については、こちらを参照してください。

原点に中心がある\(\rm{A}\)の分子が静止していたとして、半径が\(R^\ast\)の球に\(\rm{B}\)の分子が衝突してくる頻度は、球の表面積\(4\pi R^\ast\)と、動径が小さくなる方向を正とした流束\(-J\)との積であるため、\(4\pi R^\ast D_\rm{B}\)\([\rm{B}]\)と書けます。

これに\(\rm{A}\)の分子数\(VN_\rm{A}\)\([\rm{A}]\)をかけると、全体の衝突頻度が計算できます。
ここで、\(V\)は溶液の体積、\(N_\rm{A}\)はアボガドロ数です。
もちろん実際には、\(\rm{B}\)だけではなく\(\rm{A}\)の分子も拡散しているため、\(D_\rm{B}\)を2成分の拡散係数の和\(D\)として置き換えて、拡散による\(\rm{AB}\)の生成速度\(\displaystyle \frac{\rm{d}[AB]}{\rm{d}\mathit{t}}=4\pi R^\ast DN_\rm{A}\)\( [\rm{A}\)\(][\rm{B}]\)と書けます。

したがって、拡散律速の反応の反応速度定数\(k_\rm{d}\)\(=4\pi R^\ast DN_\rm{A}\)となります。

ここで、以前お話ししたストークス-アインシュタインの式を使います。
導出過程は、こちらを参照してください。

分子が球状のとき、拡散係数の和\(\displaystyle D=\frac{k_\rm{B}\mathit{T}}{6\pi \eta R_\rm{A}}+\frac{k_\rm{B}\mathit{T}}{6\pi \eta R_\rm{B}}\)と書けます。
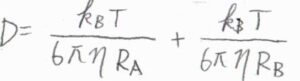
ここで、\(k_\rm{B}\)はボルツマン定数、\(\eta\)は媒質の粘性率、\(R_\rm{A}\)と\(R_\rm{B}\)は流体力学的半径です。
さらに、\(R_\rm{A}\)と\(R_\rm{B}\)の差が無視できるほど小さいとして、\(R_\rm{A}\)\(=R_\rm{B}\)\(\displaystyle =\frac{R^\ast}{2}\)と近似すると、\(\displaystyle D=\frac{2k_\rm{B}\mathit{T}}{3\pi \eta R^\ast}\)となります。
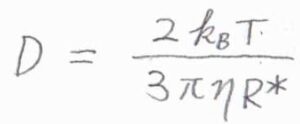
これを\(k_\rm{d}\)\(=4\pi R^\ast DN_\rm{A}\)に代入すると、\(k_\rm{d}\)\(\displaystyle =\frac{8RT}{3\eta}\)という式が導かれます。
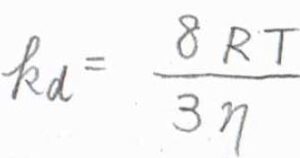
ただし、ここの\(R\)は気体定数(\(=k_\rm{B}\)\(N_\rm{A}\))なので、注意してください。
この結果より、まず反応速度は温度に比例します。
また、媒質の粘性率が大きいほど分子が移動しにくくなることで、反応は遅くなります。
そして、反応速度定数は分子の流体力学的半径には依存しません。
半径が大きいほど拡散係数は小さくなりますが、反応性の衝突半径が大きくなる効果と相殺されます。
物質収支の方程式
最後に、これまでとは反対に、反応が拡散に及ぼす影響について考えて終わります。
まずこちらは、ある物質\(\rm{J}\)について、対流も考慮して一般化した一次元の拡散方程式です。
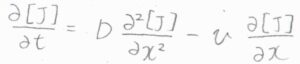
ここからさらに、\(\rm{J}\)が化学反応により消費されることを考えます。
例として、\(\rm{J}\)が擬一次反応によって消費された場合を考えると、拡散方程式の右辺に\(-k_\rm{r}\)\([\rm{J}]\)が付きます。
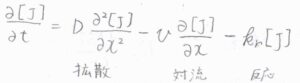
反応による物質収支を考慮して一般化された拡散方程式は、物質収支の方程式と呼ばれます。
多くの場合、この方程式を解くのは困難で、ごく限られた条件のもとでのみ解析的に解くことができます。
解析的に解けなくても、数値的に解くことで、反応容器の設計や生体内での化学反応の研究に活用されています。
解の例として、対流がない場合の物質収支の方程式の解は、こちらのようになります。
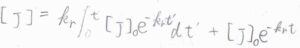
ここで、\([\rm{J}\)\(]_0\)は反応が起こっていないとき(\(k_\rm{r}\)\(=0\))の濃度です。
例として、上記の記事で示したような初期条件、境界条件では、こちらの式になります。
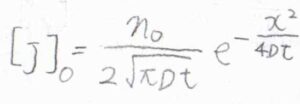
反応がある場合とない場合で比較したグラフがこちらです。
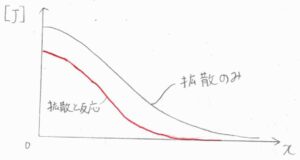
縦軸が\([\rm{J}]\)、横軸が\(x\)、黒が反応がない場合、赤が反応も起こっている場合です。
両者は拡散係数と時刻の積\(Dt\)が同じになるように濃度を重ねたものです。
反応が起こった分だけ、すべての位置で濃度は減少します。
ただ、反応によって濃度が低くなったところへ拡散が起こって分子が補充されるように、2つの効果は互いに影響を及ぼし合っているので、平行移動ではなくて、グラフの概形にも変化が生じます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




