こんにちは!
今回も化学のお話やっていきます。
今日のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(color)
では早速行きましょう!
光とは
まず、光がないと色は見えません。
広い意味での光というのは電場と磁場の揺らぎ、すなわち電磁波のことです。
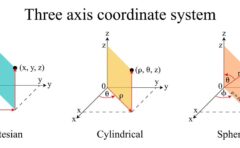
電場と磁場は、下のように互いに直交しながら進行方向に進んでいきます。

レントゲンに使われるX線や電子レンジのマイクロ波も電磁波なので、目には見えませんが、広い意味の光であると言えます。
そして、狭い意味の光というのは目に見える光、すなわち可視光のことを指します。
可視光の波長は\(380\sim 780\ \rm{nm}\)程度であり、波長によって、色が変わります。
波長\(400\ \rm{nm}\)は青、\(500\ \rm{nm}\)は緑、\(600\ \rm{nm}\)は赤色です。
蛍光灯や太陽のような白い光は、波長の異なる様々な可視光が混ざったものです。
絵の具は違う色を混ぜていくと黒色になりますが、光は混ぜていくと白色になっていきます。
色を認識する原理
仮に、ある物体に白い光が当たったとします。
そのときに、そのまますべての光が反射されれば、人は白色と認識します。
光は、網膜にあるロドプシンというたんぱく質に吸収されて、立体構造を変化させます。
それが信号となって脳に到達し、色を認識します。
では、この物体がある特定の波長の光だけ吸収してしまったとしたら、どうでしょうか?

吸収されなかった光のみが目に届くことになり、吸収された光に反応するタンパク質は、信号を脳に送らなくなります。
その結果、人は白ではない色を認識することになります。
吸収される色と人が認識する色の関係は補色と言われるもので、赤と緑、青とオレンジ、黄色と紫というような関係です。

例えば、トマトは緑の光を吸収しているので赤く見えています。
吸収波長の決まり方
続いて、吸収する光の波長がいかにして決まるのかという話をします。
結論を言うと、量子のエネルギーが不連続であることが原因です。
もし量子のエネルギーが連続であれば、すべての可視光を吸収できるので、この世のすべてのものは黒色になります。
我々が色鮮やかな世界を見ているのは、電子が波であるおかげです。
量子のエネルギーが波としての振動数に比例するという関係より、吸収波長はこのように表せます。
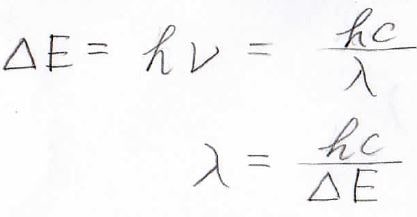
ここで、\(\displaystyle \Delta E\)は状態間のエネルギー差、\(h\)はプランク定数、\(\displaystyle \nu\)は光の振動数、\(c\)は光の速さ、\(\displaystyle \lambda\)は光の波長です。
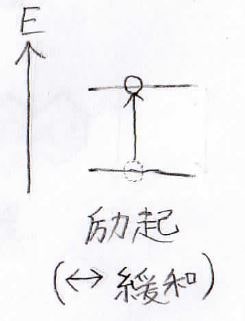
量子は光からエネルギーを得ることで、高いエネルギー状態に遷移します。
この遷移のことは励起と呼びます。
逆は緩和といいます。
モデルを使った計算
ここからは、モデルを使って、光の吸収を考えていきます。
井戸型ポテンシャル
まず、一次元井戸型ポテンシャルに拘束された電子について考えます。
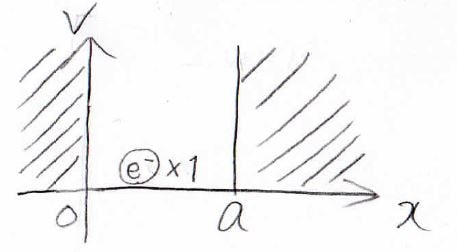
井戸型ポテンシャルについて、詳しくはこちらの記事で解説しています。

エネルギーは、下の式で与えられます。
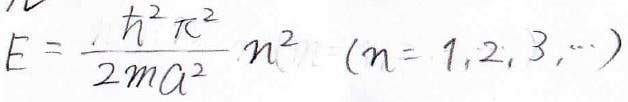
これを図で書くと、下のようになります。
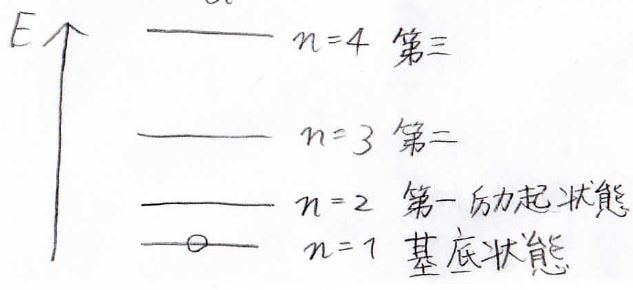
最もエネルギーが低い状態のことは基底状態と呼び、それ以外をエネルギーが低いものから第一励起状態、第二励起状態と呼びます。
\(n\)が\(n_1\)から\(n_2\)へ遷移したときに吸収した電磁波の波長は、下の式で与えられることになります。
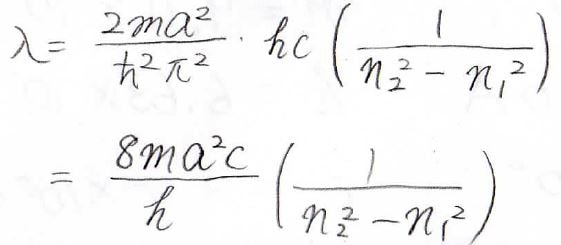
最も状態間のエネルギー差が小さいのは、\(n\)が\(1\)から\(2\)に遷移するときなので、そこから最大の吸収波長も計算できます。
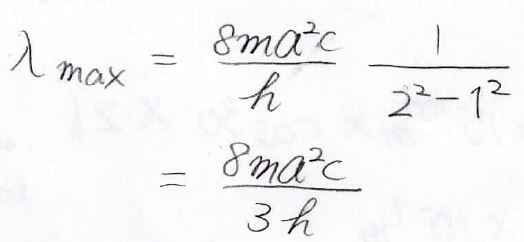
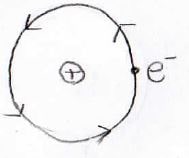
ボーアの原子モデル(水素原子)
続いて、ボーアの原子モデルもやってみましょう。
水素原子の周りを等速円運動する電子のエネルギーは、下の式で書けます。
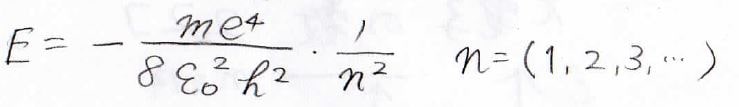
そのため、吸収波長の逆数は、下の式で与えられます。
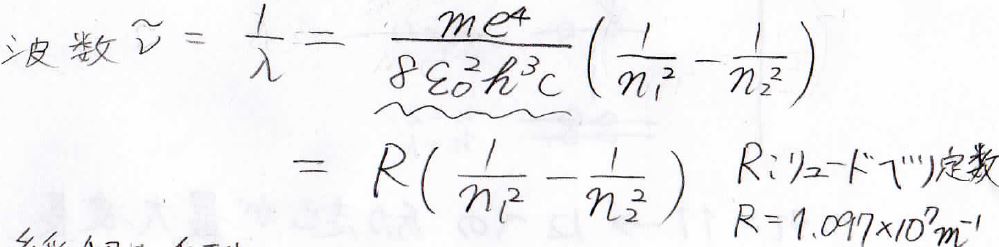
波長の逆数は波数と呼ばれ、エネルギーの単位として扱われることが多いです。
この波線部分には名前が付いており、リュードベリ定数と言います。
その値は\(1.097\times 10^7 \ \rm{m}^{-1}\)です。
緩和について
ここまではずっと、光の吸収、つまり励起の話をしていましたが、エネルギーの放出、つまり緩和の話も少ししておきます。
緩和の際に放出されるエネルギーの形は光とは限らなくて、熱の場合もあります。
太陽の光を温かいと感じるのは、太陽の熱が直接届いているわけではなく、太陽光を吸収した我々の体が緩和により発熱するからです。
高校の物理で習いますが、上記のリュードベリ方程式において、遷移には名前が付いており、\(n_1=1\)、すなわち高いエネルギー状態から基底状態まで緩和してきたときの遷移系列のことをライマン系列と呼びます。
\(n_1\)が\(2\)のときはバルマー系列、\(n_1\)が\(3\)のときはパッシェン系列と言います。
練習問題
最後に、練習問題をやってみましょう。
ニンジンの色素として有名な\(\displaystyle \beta\)-カロテンという物質があります。
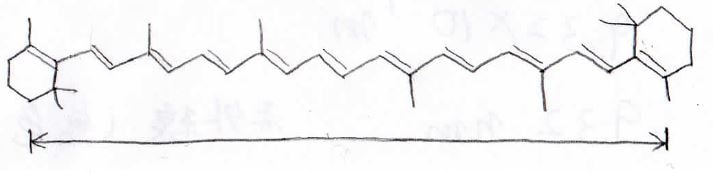
その構造はここにあるとおり、とても長い\(\displaystyle \pi\)電子共役系をもっています。
\(\displaystyle \pi\)電子共役系についてはこちらの記事をご覧ください。
では、この\(\displaystyle \pi\)電子共役系を井戸型ポテンシャルに見立てて吸収波長を計算したとき、\(\displaystyle \beta\)-カロテンは何色に見えると予想されるでしょうか?
いわばニンジンの色を計算してくださいということです。
計算に使うパラメータは、下記のとおりです。
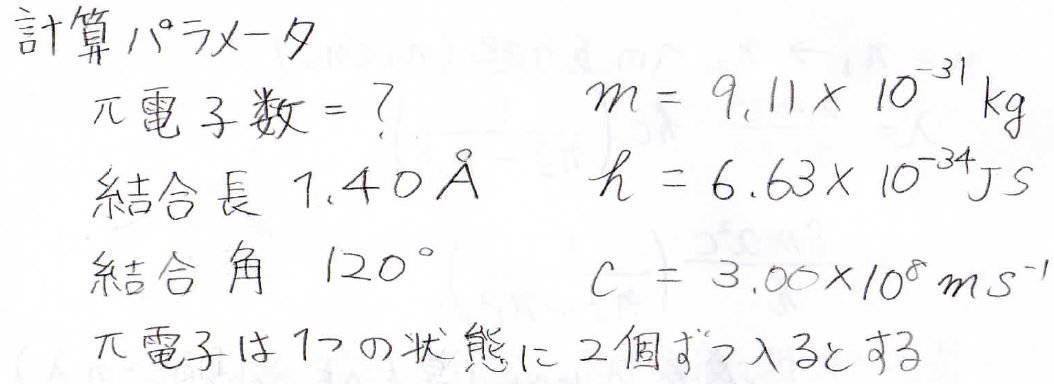
\(\displaystyle \pi\)電子の個数は自分で数えてください。
また、井戸型ポテンシャルの各状態には、電子が2個ずつまで入れるということにします。
詳しくはこちらの記事をご覧ください。
パウリの排他原理とスピン量子数について説明しています。
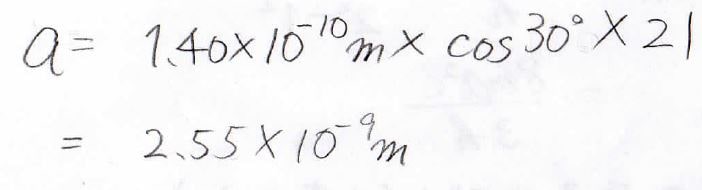
\(\displaystyle \pi\)電子の数を数えると22個になるので、\(n=11\)の状態まで電子が入っていることになります。
したがって、\(n=11\)からの遷移を考えればOKです。
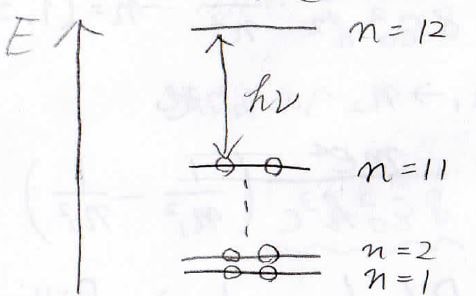
まず最大吸収波長は\(n=11\)から\(12\)への遷移ですが、計算してみると\(932\ \mathrm{nm}\)となって、赤外線になります。
そのため、色としては認識できません。

次に、2番目に長い波長を求めます。
\(n=11\)から\(13\)への吸収波長は\(447\ \rm{nm}\)となりました。
これは青色の光です。
目に見える色は青色の補色であるオレンジ色という結果になります。
3番目に長い波長については\(286\ \mathrm{nm}\)で、これは紫外線なので色として認識できません。

したがって、\(\displaystyle \beta\)-カロテンが主に吸収するのは青い光で、実際に認識される色はオレンジ色と計算できました。
このように、\(\displaystyle \beta\)-カロテンのように長い\(\displaystyle \pi\)電子共役系をもっている分子は、可視光を吸収することが多いです。
例えば、下に書いたのはベンゼン環が直鎖上につながったアセンという化合物ですが、長くなるにつれて、色が付いていって、黒っぽい色になっていきます。
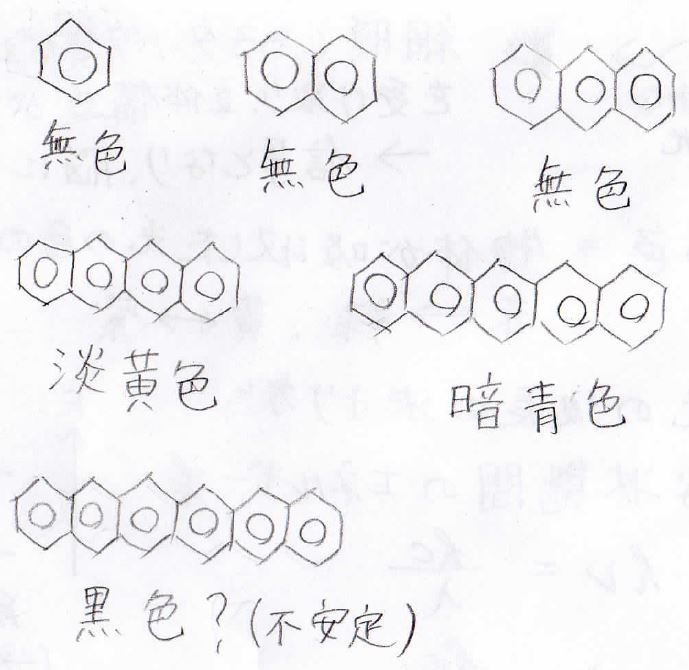
黒色に近いのは、可視光領域に複数の吸収波長があることを意味しています。
ただし、今回やったように井戸型ポテンシャルの計算でこれらの色を予測しても、正確な色と違う結果が出てきます。
今回やった計算はとても大雑把で、井戸型ポテンシャルで予想される色は正確ではありません。
実際はもっと複雑な計算をする必要があります。
\(\displaystyle \pi\)電子共役系のエネルギー準位を計算する方法については、以下の記事で説明しています。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!