こんにちは!
それでは今回も数学の続きをやっていきます。
今日のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(determinant meaning)
では、内容に行きましょう!
正則行列の判定
まず、行列式は逆行列が存在するかどうかの判定に使うことができます。
逆行列が存在する正方行列のことは正則行列と呼ばれ、ここに示すような条件を満たします。

今回証明はしませんが、これらの条件は同値であるため、どれか1つ満たしていれば同時に他のすべての条件を満たすことになります。
そして、この5つ目にあるように行列式の値が\(0\)ではないときに逆行列は存在し、逆行列が存在するなら行列式は\(0\)になりません。
例えば、下の行列式は\(0\)になるので、正則行列ではないことが言えます。
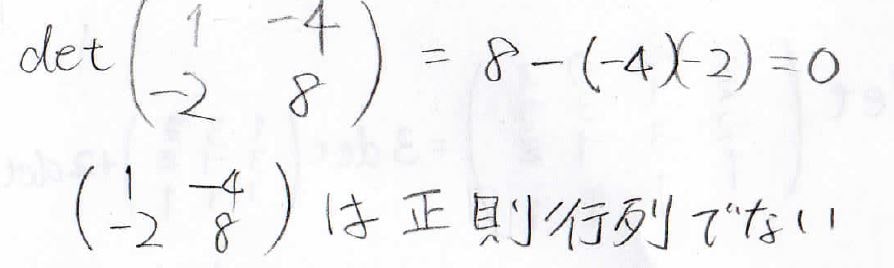
行列式と幾何の関係
ここからは、行列式と幾何、つまり図形の問題との関係について考えていきましょう。
2つのベクトルで張られる平行四辺形の面積
まず、2次元平面に置いて2つの縦ベクトル \(\boldsymbol{a}_1\)と\(\boldsymbol{a}_2\)があったとします。
このとき、 \(\boldsymbol{a}_1\)と\(\boldsymbol{a}_2\)を並べた行列の行列式の絶対値は、2つのベクトルで張られた平行四辺形の面積と等しくなります。
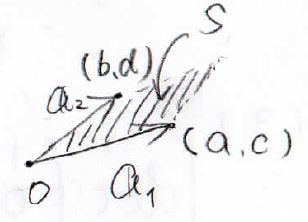
\(\boldsymbol{a}_1\)を\((a,c)\)、\(\boldsymbol{a}_2\)を\((b,d)\)、2つのベクトルがなす角を\(\theta\)として証明を考えます。
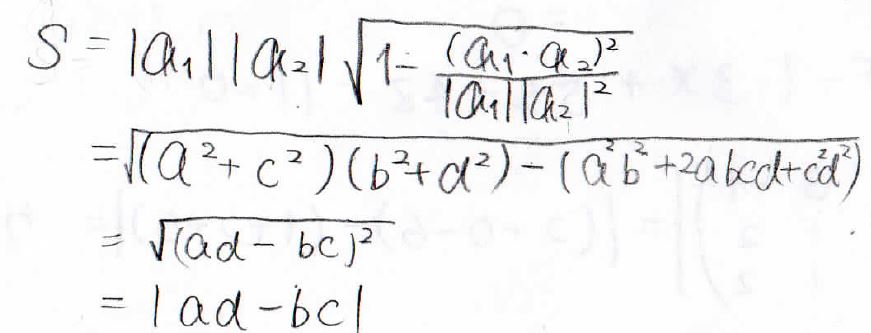
平行四辺形の面積は、それぞれの辺の長さの積に\(\sin{\theta}\)をかけたものになります。
これを変形していくと、この面積が\(ad-bc\)となり、確かに行列式の値と等しくなることがわかります。
3つのベクトルで張られた平行六面体の体積
では、同じことを3次元で考えてみましょう。
3つの3次元縦ベクトル\(\boldsymbol{a}_1\)、\(\boldsymbol{a}_2\)、\(\boldsymbol{a}_3\)を並べた行列の行列式の絶対値は、この3つのベクトルで張られる平行六面体の体積と等しくなります。

ここで、その体積は\(V\)とおいておきます。
\(\boldsymbol{a}_1\)と\(\boldsymbol{a}_2\)の外積について考えると、底面積がその絶対値で与えられることになります。
また、その外積と \(\boldsymbol{a}_3\)がなす角を\(\theta\)とすると、底面と\(\boldsymbol{a}_3\)がなす角は\(\displaystyle \frac{\pi}{2}-\theta\)になります。
体積\(V\)は底面積と高さの積なので、結局は\(\boldsymbol{a}_1 \times \boldsymbol{a}_2\)と\(\boldsymbol{a}_3\)の内積になります。

ここで、行列式について考えてみます。

まず、この行列式を3列目に対して余因子展開します。
このやり方については、前回までの記事を見てください。


すると、余因子行列の部分は、 \(\boldsymbol{a}_1 \times \boldsymbol{a}_2\)と等しくなります。
さらに\((a_{13}, a_{23}, a_{33})\)は、ベクトルの\(\boldsymbol{a}_3\)なので、ベクトルの内積に書き換えることができ、先ほど変形した体積\(V\)と等しいことになります。
以上の考え方は、変数の変換を伴う多変数関数の積分にも応用されます。
詳しくは、こちらを参照してください。

3点が同一直線状にあるかどうかの判定
そして、行列式は、同一直線上、同一平面上にあるかどうかの判定に用いることができます。
まずは直線についてお話ししますが、平面上のある3点が同一直線上の点だったとき、それぞれの座標を縦に並べて3行目に\(1\)を並べた行列式が\(0\)になります。
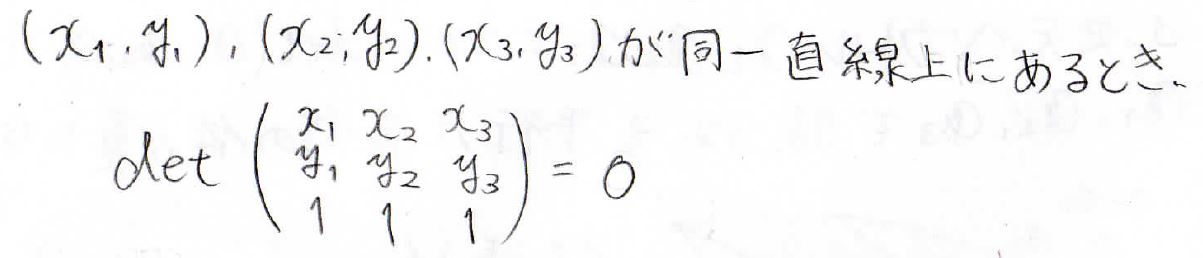
これはなぜかというと、仮に3点が直線\(ax+by+c=0\)上の点だったとき、この連立方程式を満たす\((a,b,c)\)の組がすべて\(0\)というもの以外に存在することになります。

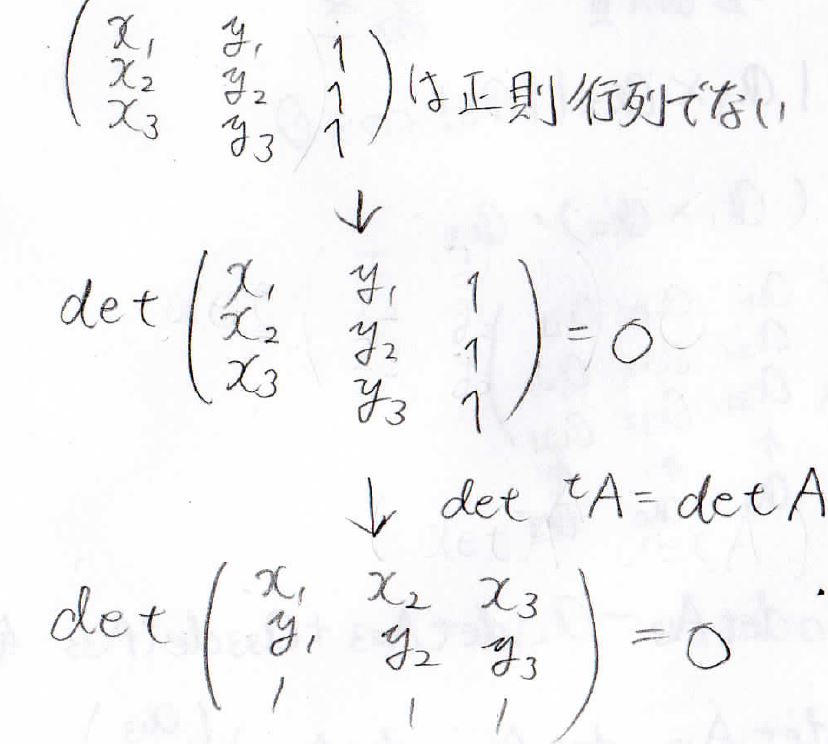
すべて\(0\)であれば、直線の式にはなりません。
そして、この行列が仮に正則行列だった場合は、ただ1つの厳密解が得られ、右辺が零ベクトルのときの解は零ベクトルしかないことになります。
したがって、この行列は正則行列ではないことになり、その行列式の値は\(0\)になります。
そして、転置行列の行列式が元の行列式と等しいという関係を使うと、上記の行列式が\(0\)であるということになります。
4点が同一平面上にあるかどうかの判定
同一平面上にある4点にも同じことが言えます。
この行列式が\(0\)になったとき、その4点は同一平面上にあることが示せます。

練習問題
最後に、今回紹介した行列式と幾何の関係を実際に使ってみましょう!
今回は2問の練習問題を用意しました。

(1)上記の3点が通る平面の式は?
高校の知識でもできますが、ぜひ行列式をどう使ったら求められるのか考えてみてください。
(2)上記の3つのベクトルで張られた平行六面体の体積は?
すると、今回話した内容より、この行列式が\(0\)になればよいということになります。

あとは次数下げや余因子展開によって計算していけば、最終的に\(3x+5y4z-11=0\)という式を得ることができました。
(2)では、素直に\(3\)次行列式をサラスの方法を用いて解くだけです。
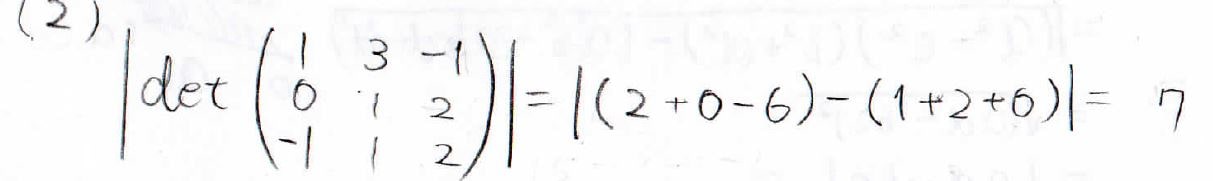
サラスの方法についてはこちらで解説しています。

行列式の値は\(-7\)になって、平行四辺形の面積はその絶対値になるので、\(7\)と計算できます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




