こんにちは!
今日も化学のお話やっていきましょう。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(hydrogen 1、hydrogen 2、hydrogen 3、hydrogen 4)
それでは早速内容に入っていきましょう!
(動画Part 1の内容)
シュレディンガー方程式の限界
実は、シュレディンガー方程式では多体問題を厳密に解くことができません。
シュレディンガー方程式の導出過程については、こちらもあわせてご覧ください。

原子は、原子核と電子という少なくとも2個以上の量子から構成されるので、厳密な計算はできないということになります。
ただそれでは困るので、何とか近似をして計算できるようにする方法が提案されました。
その方法は、ボルン=オッペンハイマー近似と言います。
陽子の質量は電子の約1840倍なので、原子核の運動は電子に比べると、非常に遅いことになります。
そこで、原子核の運動は止まっていて、電子だけの計算をすればよいとしたのが、このボルン=オッペンハイマー近似です。
こうすることで、電子が1個のときだけ計算ができるようになります。
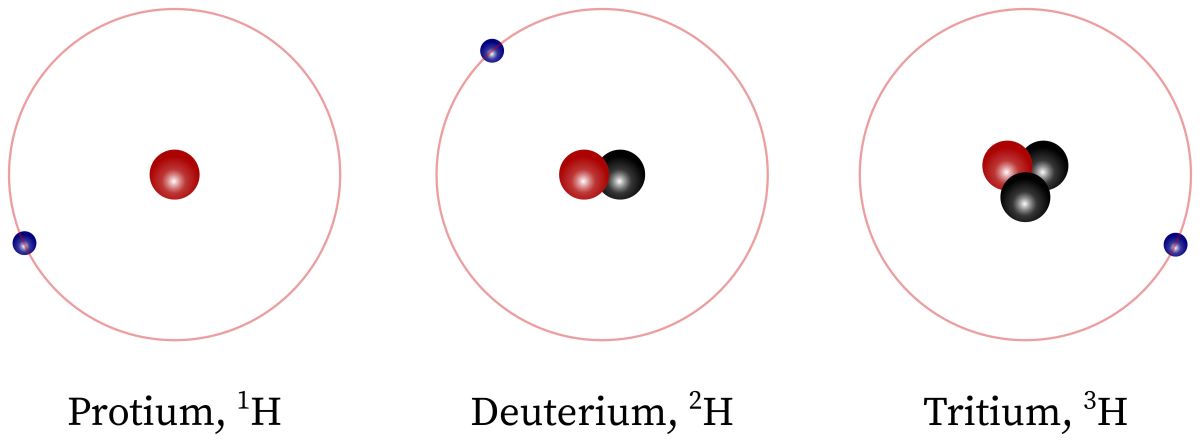
例としては、\(\displaystyle \rm{H}\)や\(\displaystyle \rm{He}\)\(^+\)、\(\displaystyle \rm{Li}\)\(^{2+}\)などで、これらは水素様原子と呼ばれます。
水素原子について解けば、あとは原子核の電荷を変化させればよいだけなので、ここからは水素原子について考えていきます。
水素原子のシュレディンガー方程式
水素原子のシュレディンガー方程式は、以下のとおりに書けます。
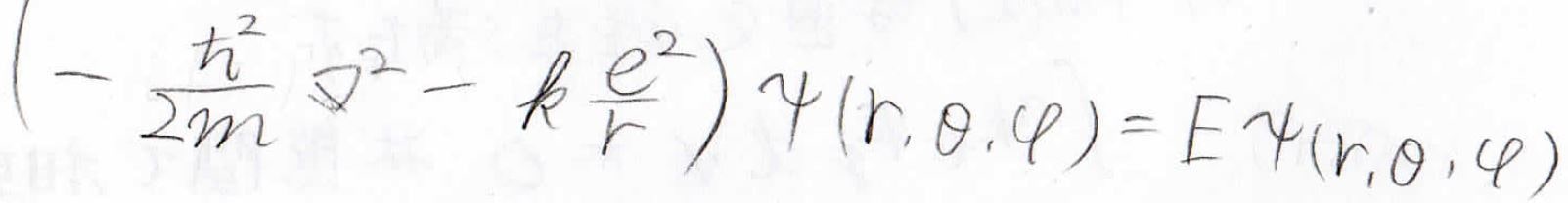
ここから少しテクニカルなのですが、波動関数\(\psi\)が長さのパラメータ\(r\)の関数と角度のパラメータである\(\theta\)と\(\varphi\)の関数の積として分けられると考えます。

この\(R\)は動径波動関数、\(Y\)は球面調和関数といいます。
\(\boldsymbol{\nabla} ^2\)も極座標表示にします。
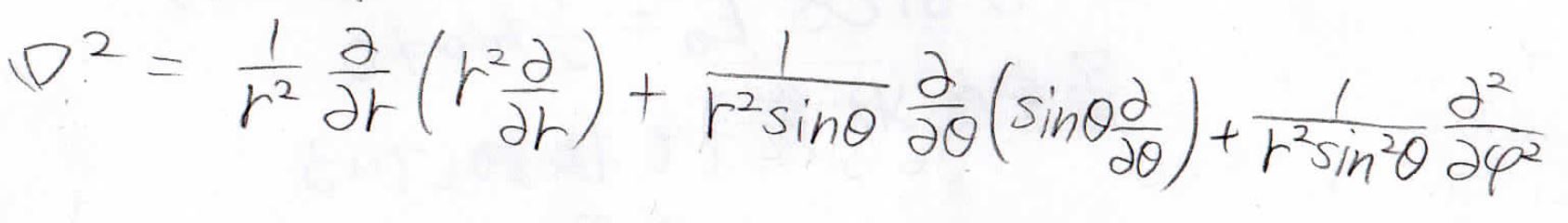
詳しくはこちらの記事をご覧ください。
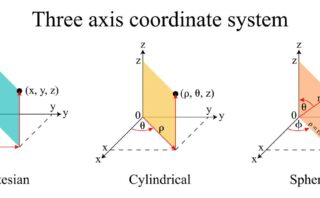
波動関数\(RY\)を\(\psi\)に代入すると、下の形になります。
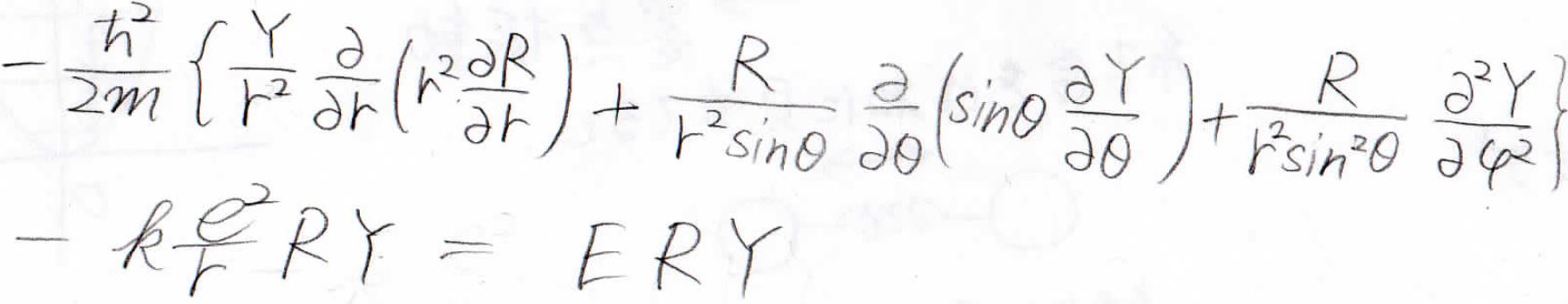
ここから、この式を変形していきます。
まず、この式を整理すると、下の形になります。
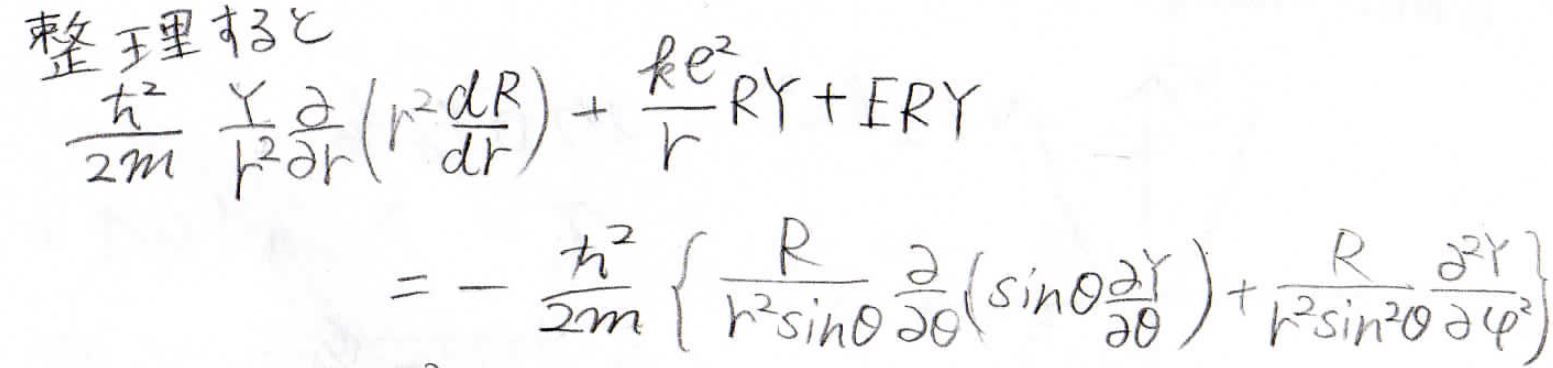
これの両辺に\(\displaystyle \frac{2mr^2}{RY}\)をかけます。
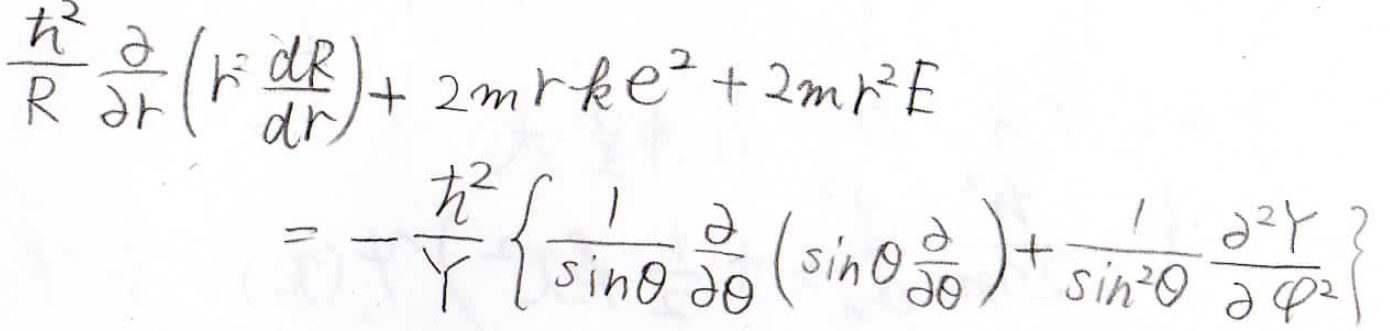
この式をよく見てみると、左辺には角度パラメータがなく、動径\(r\)だけの関数になっています。
そして、右辺は角度だけの関数になっています。
この等号が常に成り立つということは、この値がパラメータに依存しない定数だということになります。
したがって、この式の左辺を定数\(\Lambda\)と置くことができます。
さらに、球面調和関数が\(\theta\)と\(\varphi\)それぞれの関数の積で与えられると仮定して、変形します。
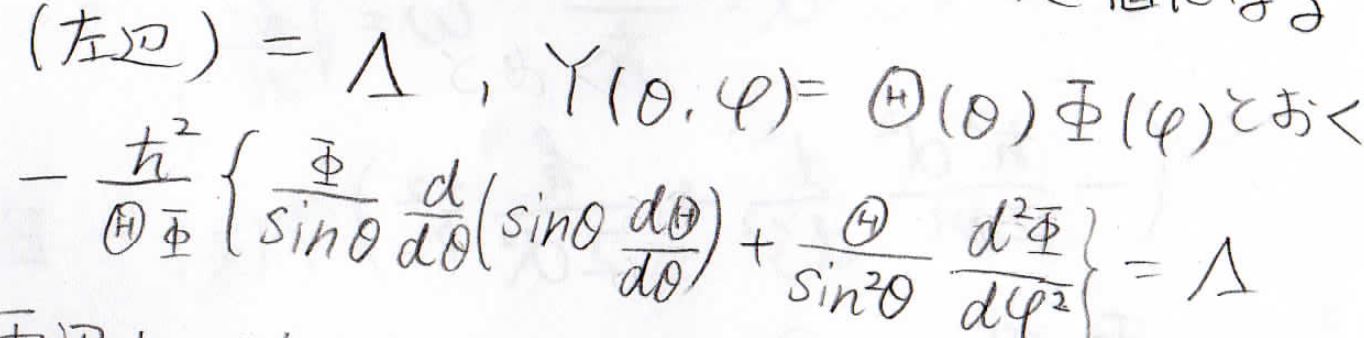
この式でも左辺は\(\theta\)だけ、右辺は\(\varphi\)だけという形にできるので、またこれを定数\(\displaystyle \nu\)と置きます。
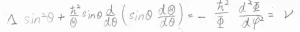
すると、\(\varphi\)について微分方程式が得られます。
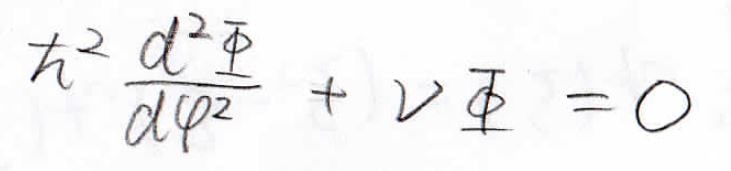
微分方程式については、こちらをご覧ください。

これを解くと、下のようになります。

ここで、極座標での\(\varphi\)は\(xy\)平面上の角度なので、\(2\pi\)で一周したことになります。
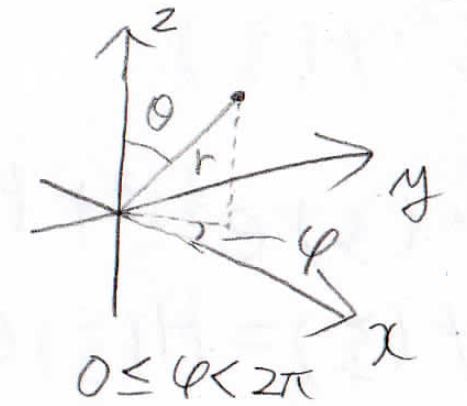
したがって、\(\Phi(\varphi)=\Phi(\varphi+2\pi)\)という関係が成り立ちます。
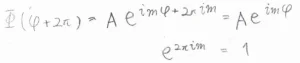
この関係式を満たす条件は、\(\cos (2\pi m)=1\)かつ\(\sin (2\pi m)=0\)より、\(m\)が整数のときということになります。
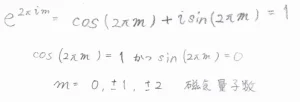
この整数\(m\)のことは、磁気量子数と言います。
最後、規格化条件から\(A\)を実数として求めると、\(\displaystyle \Phi (\varphi)=\frac{1}{\sqrt{2\pi}}\rm{e}\)\(^{\rm{i}\mathit{m\varphi}}\)となります。
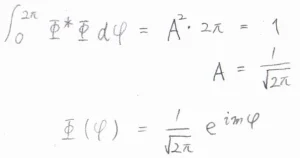
(動画Part 2の内容)
角運動量
まず、角運動量というものについてお話します。
角運動量とは、回転運動を考える際に便利な量で、位置ベクトルと運動量ベクトルの外積で定義されます。


角運動量には、エネルギーや運動量同様、保存則が成り立つことが知られています。
角運動量は外積、つまりベクトルなので、大きさだけでなく方向も含めて保存されます。
角運動量の方向が保存されることを利用しているのが自転車です。
ゆっくり漕いだときだけ左右にふらつくのは、角運動量の大きさが小さく、人が及ぼす外力の影響が大きくなるからです。
速く漕いだときに軸の方向が安定する効果のことは、ジャイロ効果と呼びます。
水素原子中の電子の角運動量
ではここからは、水素原子中の電子の角運動量を考えていきます。
まず、3次元での角運動量演算子は、このように表すことができます。
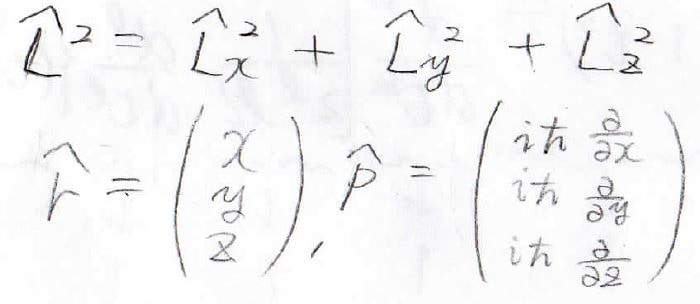
それぞれの成分は、位置ベクトルと運動量演算子を使って、外積の計算から導くことができます。
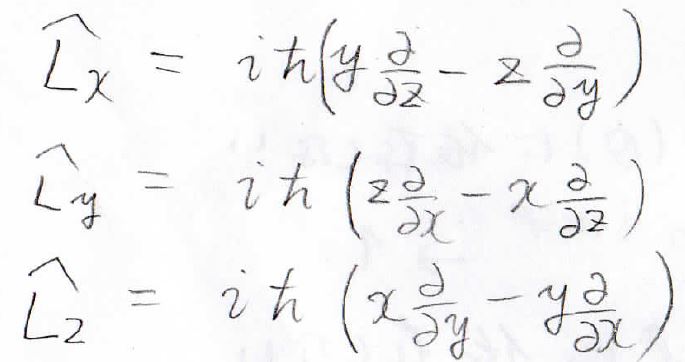
これを極座標にすると、こちらのようになります。
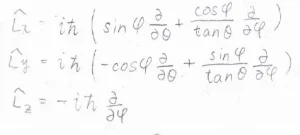
この結果より、全体の軌道角運動量演算子\(\displaystyle \hat{L}^2\)は、極座標で以下のように表されます。
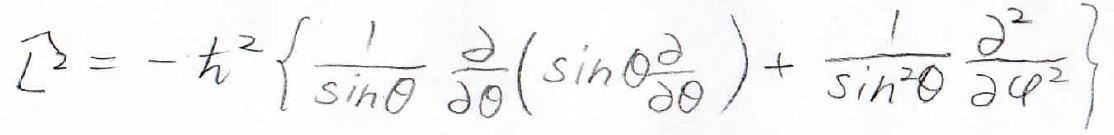
Part 1の中で出てきた式を思い出してみると、そのまま角運動量演算子が入っています。
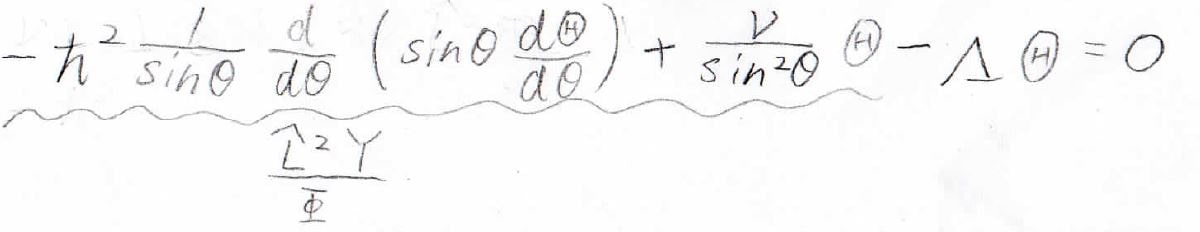
この式に、\(\nu= m^2\hbar^2\)を代入します。
また、\(\displaystyle \lambda\)を定数として、\(\Lambda=\hbar ^2\lambda\)と書き換えます。
すると、先ほどの式は下のような形になります。
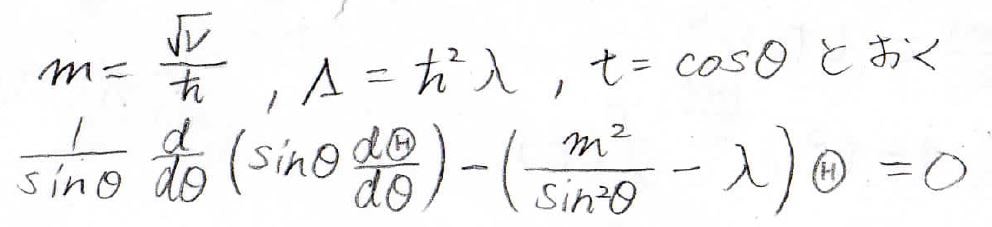
\(\cos{\theta}\)を\(t\)で置き換えると、このような形になります。
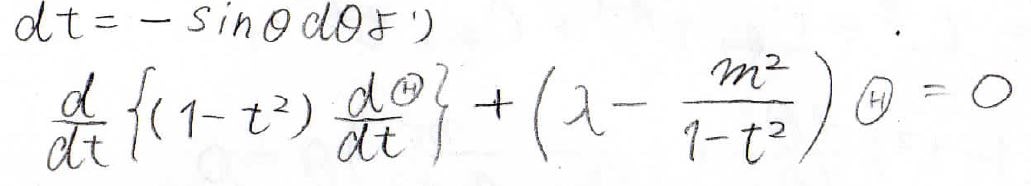
複雑な式ですが、ここで\(\Theta\)を\(t\)のべき級数で表すことを考えます。
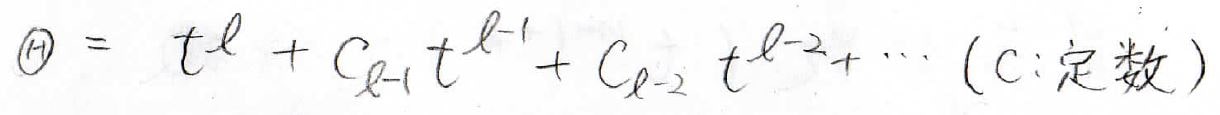
ここで、最高の次数は\(l\)としています。
まず、簡単な場合として、\(m=0\)のときについて考えてみます。
すると、下の式が成り立つわけですが、ここで\(t\)についての最高次数の項だけに注目してみます。
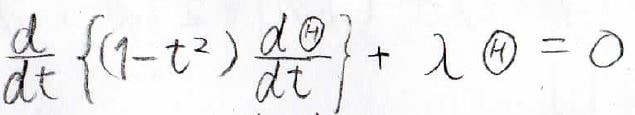
最も次数が大きい\(\displaystyle t^l\)の係数は、このようになります。
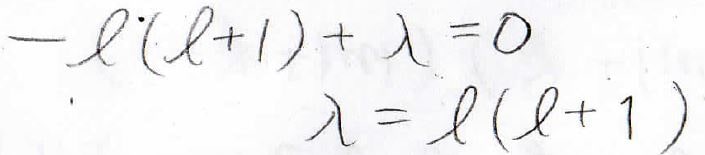
右辺が\(0\)ということから、すべての係数が\(0\)になるはずなので、この値も\(0\)になるということになります。
この関係より、\(\lambda=l(l+1)\)ということがわかります。
これ以降の計算過程は複雑なため結果だけを示すと、\(\Theta\)は下記の関数に比例するということになります。
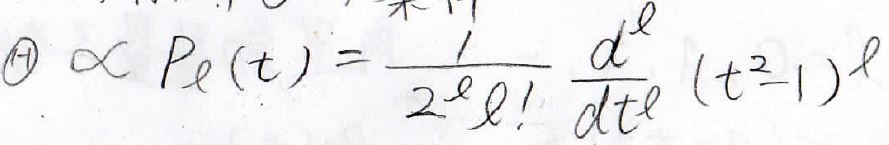
この\(P_l(t)\)のことは、ルジャンドル多項式と呼びます。
また、\(m=0\)ではないときについて考えると、次のようになります。
これもテクニカルなのですが、\(\alpha\)を定数として、\(\Theta\)を\((1-t^2)^\alpha \times\)(何らかの関数)という形で表現したとします。

このときに\((1-t^2)^{\alpha-1}\)の係数部分を考えると、下の関係式が得られます。
\(t\)が\(1\)に近い値のときには、\(4\alpha^2-m^2=0\)という関係になります。
そして、\(\displaystyle \alpha=\frac{|m|}{2}\)とすれば、\(\Theta\)を下の形で表現できます。
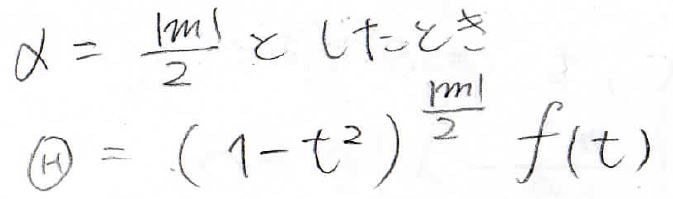
ここで、\(f(t)\)は\(t\)に関する未知の関数です。
先ほどと同じように、\(f(t)\)が\(t\)のべき級数で表せると仮定して、最高次数の項の係数を求めてみるとこのようになります。
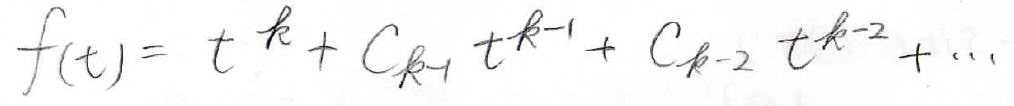
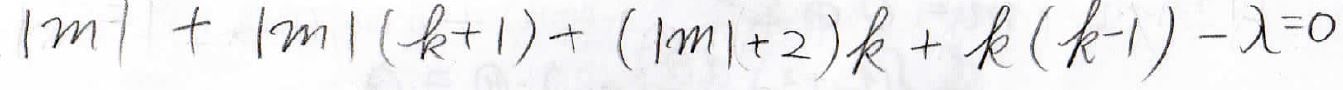
\(\lambda=l(l+1)\)でしたが、\(m\)と\(k\)を使うと、下のようにも表現できることになります。
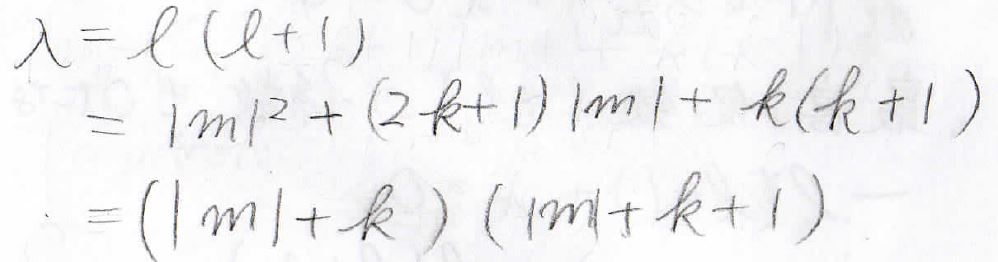
以上より、\(l=|m|+k\)という関係がわかります。
\(k\)が\(0\)か自然数であることから、\(l\)と\(m\)の関係は、\(|m|\leqq l\)となります。
\(l\)は、(軌道)角運動量量子数または方位量子数と呼ばれ、\(0\)か自然数をとります。
方位量子数と磁気量子数の関係は、電子の数が2個、8個、18個…で閉殻の状態になることを説明するのに重要となります。
詳しくは、本記事の練習問題の解答をご覧ください。
結局のところ、\(\Theta\)は\(m\)と\(l\)を使って、下のように表されます。
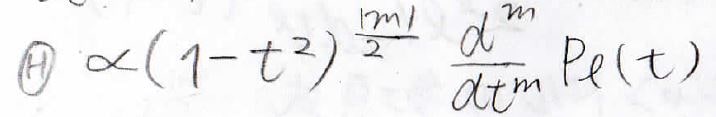
最後に規格化定数を求めれば、球面調和関数を求めることができます。
多変数関数の重積分で、座標系を変えた場合には、ヤコビアンもかけて積分します。
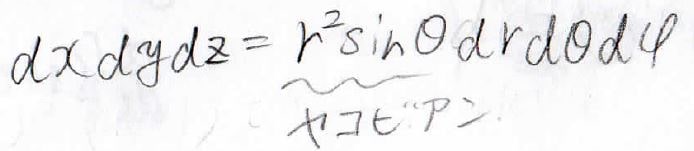
詳しくはこちらをご覧ください。

最終的に得られた球面調和関数の例を示すと、以下のようになります。

(動画Part 3の内容)
動径関数
ここからは、\(\displaystyle r\)にのみ依存する動径波動関数\(\displaystyle R(r)\)について、考えていきます。
まず、シュレディンガー方程式の両辺を球面調和関数で割ったものが、こちらの式になります。
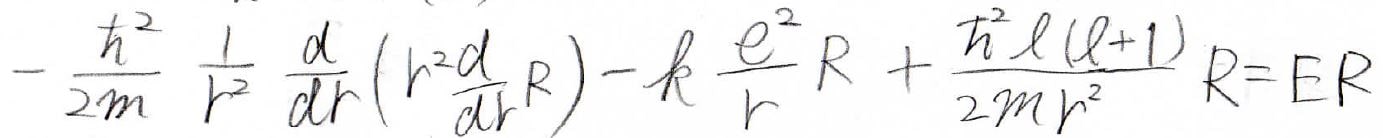
ここで、\(\hbar ^2l(l+1)\)というのが、角運動量の大きさの2乗に相当します。
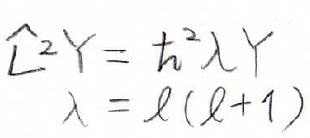
ここから変形を始めていくわけですが、まずは距離\(r\)を長さの次元を持つ量で割って無次元化します。
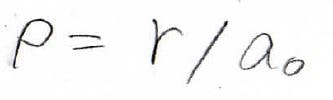
それを\(\rho\)と置きます。
ここで\(a_0\)は、ボーア半径としておきます。
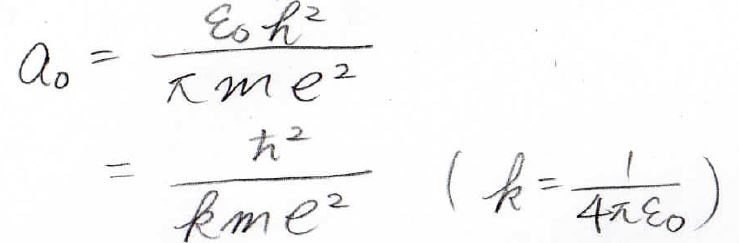
上式で、\(\displaystyle \varepsilon_0は\)真空の誘電率、\(\displaystyle m\)は電子の質量、\(\displaystyle e\)は電気素量です。
変数を\(r\)から\(\rho\)にすると、上の式はこのようになります。
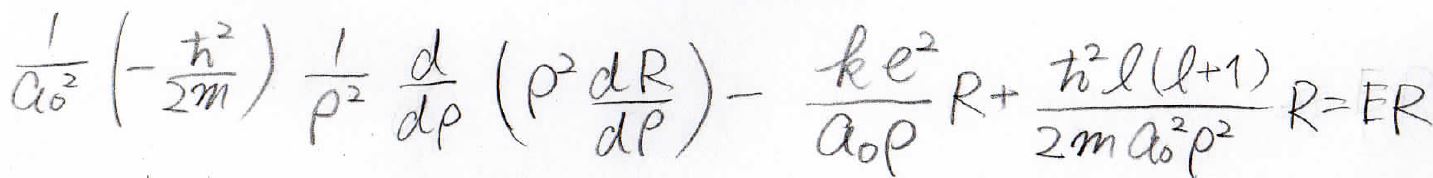
両辺に\(\displaystyle -\frac{2ma_0^2}{\hbar ^2}\)をかけると、このようになります。
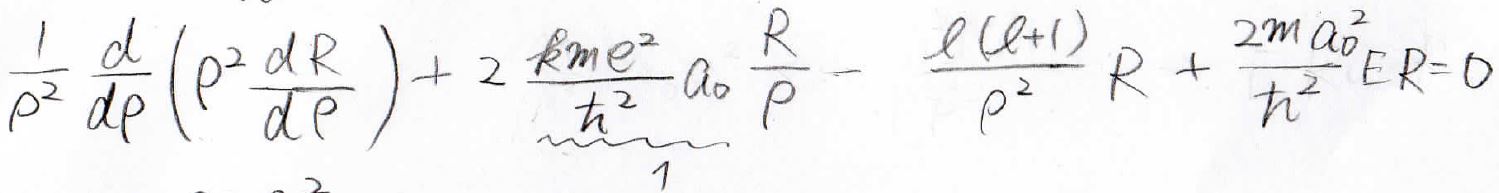
\(\displaystyle -\frac{2ma_0^2}{\hbar ^2}E\)を\(\varepsilon\)と置いて、さらに変形します。

ボーア半径の式より、上式の波線部は\(1\)になるので、ここまで簡単な形に変形させることができます。
これを満たす関数\(R\)を求めるために、まずは\(R\)をべき級数数に展開したときの最小次数について考えてみます。
その次数を\(t\)とすると、\(\rho\)が\(0\)に近い値のときには、\(R\)が\(\rho^t\)に比例すると考えることができます。
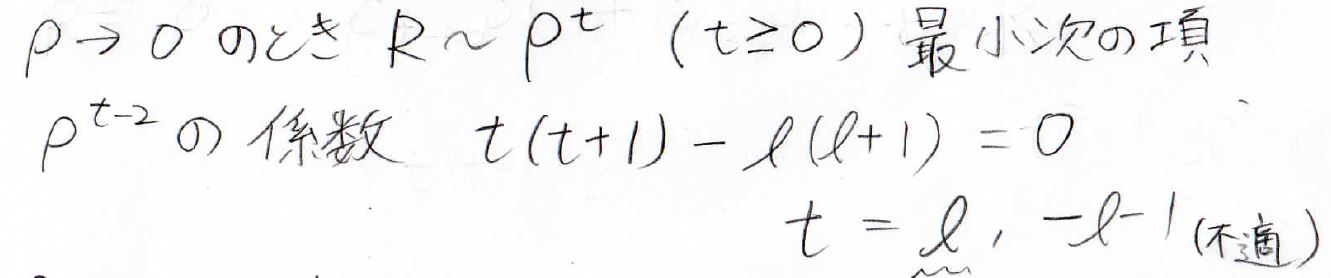
先ほどの式で、最低次の項は\(\rho ^{t-2}\)であり、その係数は\(t(t+1)-l(l+1)\)となります。
これが\(0\)になるためには、\(t\)が\(l\)もしくは\(-l-1\)となる必要があります。
\(t\)も\(l\)も\(0\)以上なので、\(t\)は\(l\)と等しいとわかります。
では今度、反対に\(\rho\)が無限大の場合を考えてみましょう。
\(\displaystyle \frac{1}{\rho}\)、\(\displaystyle \frac{1}{\rho ^2}\)の項は無視できるとして、2つの項だけが残ってきます。
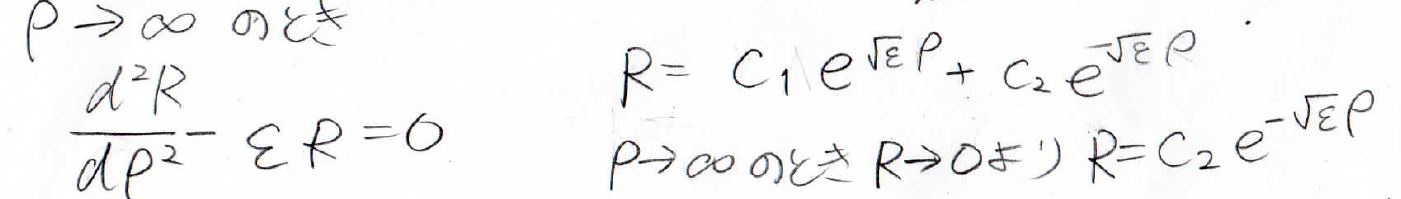
これは簡単に解ける微分方程式で、上のような解が得られます。
ここで、\(r\)が無限大のとき、すなわち原子から無限に離れたときには、電子の存在確率が\(0\)になるというのが、境界条件になります。
電子が原子核の拘束を受けないほど離れてしまったら、それはもはや原子ではありません。
よって、\(\rm{e}\)のマイナス乗の項だけが残ってくることになります。
ここまでの情報から、\(R\)は\(\rho ^l\)と\(\exp{(-\sqrt{\varepsilon}\rho)}\)に比例することがわかったので、このように書くことができます。
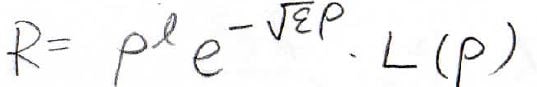
\(R\)がこれらの関数の定数倍であるとは限らないので、あまりの\(\rho\)の関数を\(L(\rho)\)としています。
では最後、この\(L(\rho)\)を求めてみましょう。
上記の内容と同様に、べき級数で書いてみましょう。
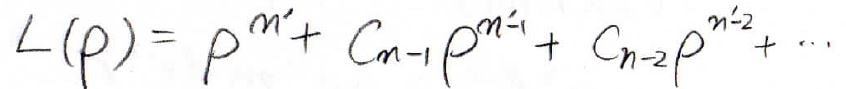
最高次数を\(n’\)としておきます。
まず、\(n’=0\)のときについて、シュレディンガー方程式の\(\displaystyle \rho^{l-1}\exp{(-\sqrt{\varepsilon}\rho)}\)の項の係数を考えます。
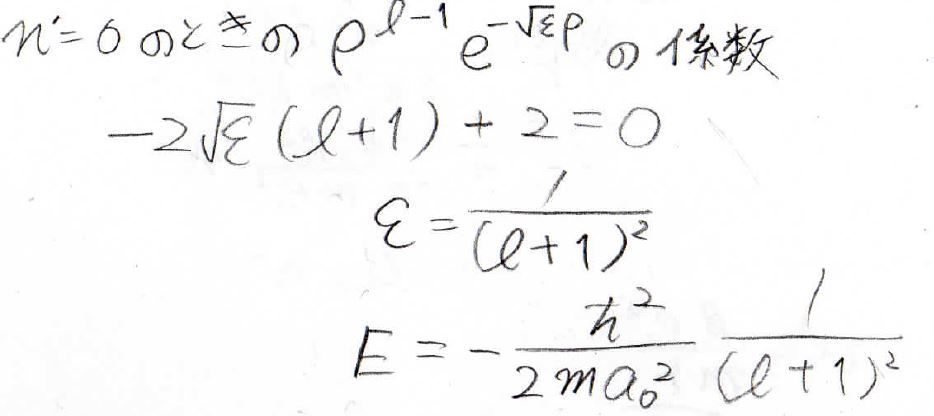
最高次数ではないのですが、\(\rho ^{l-1}\)の係数について考えることで、電子のエネルギーが求められます。
実際に微分して、その係数を\(0\)とすると、\(\displaystyle \varepsilon=\frac{1}{(l+1)^2}\)となります。
\(\displaystyle \varepsilon=-\frac{2ma_0^2}{\hbar ^2}E\)だったので、ここからエネルギーが得られます。
では今度、\(n’\)が\(0\)ではないときについて考えると、\(\rho ^{n’+l-1}\)の係数は下のようになるので、同様にエネルギーを\(n’\)と\(l\)を使った形で表すことができます。
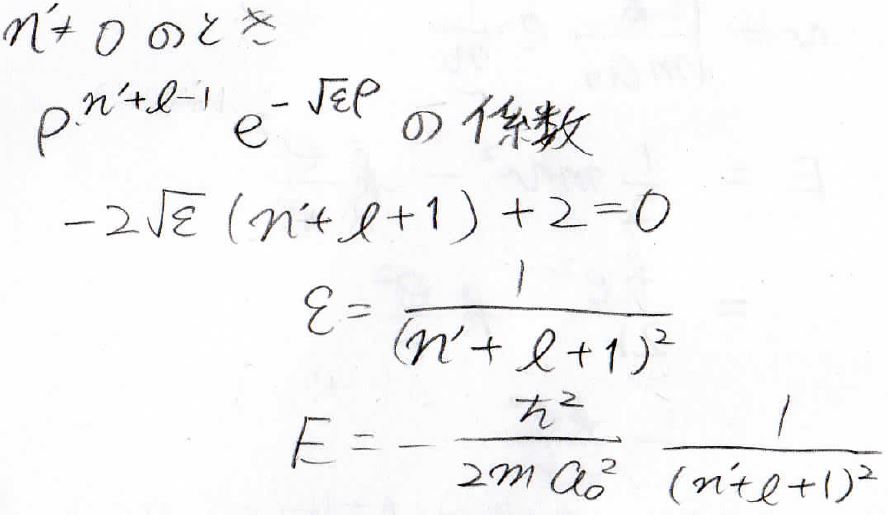
ここで、\(n’+l+1=n\)とすると、水素原子中の電子のエネルギー準位を求めることができます。
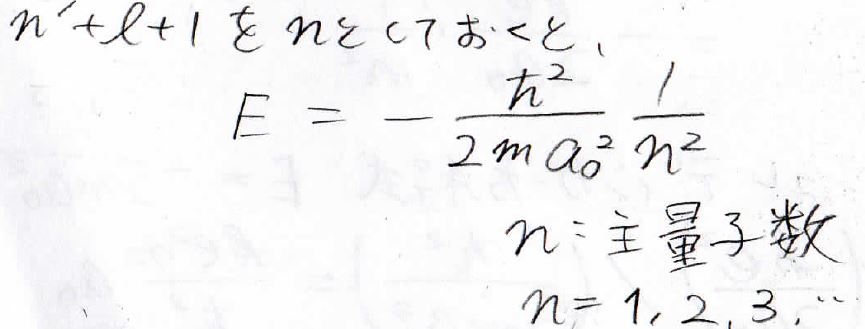
この\(n\)は主量子数と呼ばれ、水素様原子のエネルギーは、主量子数のみで決まることになります。
方位量子数\(l\)や磁気量子数\(m\)が変わったときには、波動関数の形状や方向は変わってもエネルギーは変わりません。
(動画Part 4の内容)
量子数のまとめ
ここで、これまでの話で出てきた量子数についてまとめてみます。
シュレディンガー方程式からは3種類の量子数が出てきて、それぞれ主量子数、軌道角運動量量子数(または方位量子数)、磁気量子数と呼ばれます。
これらはそれぞれ\(n\)、\(l\)、\(m\)という文字で表されることが多いです。
しかし、考えるべき量子数はこれですべてではなく、スピン量子数\(s\)と呼ばれるものがあります。
地球の自転と同じように量子もそれ自身が回っていて、シュレディンガー方程式で求められる軌道角運動量とは別の角運動量をもつことが知られています。
古典的なイメージとしては、電荷を持っている粒子が自転したときに、下図の向きに磁場が発生するようなものです。
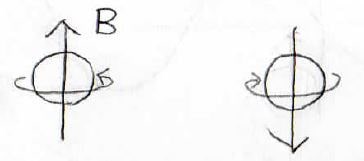
その値が\(\displaystyle \frac{1}{2}\)や\(\displaystyle \frac{3}{2}\)などの半整数をとる場合と、\(1\)や\(2\)などの整数をとる場合で、挙動が大きく変わることが知られており、前者はfermi粒子、後者はbose粒子と呼びます。
またfermion、bosonとも呼びます。
電子はfermi粒子の1つで、\(s\)は\(\displaystyle \frac{1}{2}\)もしくは\(\displaystyle -\frac{1}{2}\)という値をとります。
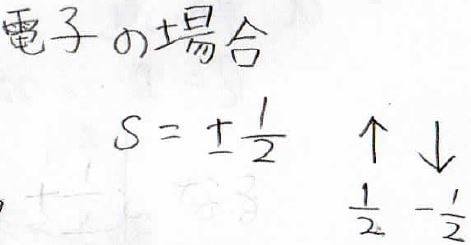
ここで、軌道という言葉の説明をします。
これは1つの電子の分布を指した言葉で、\(n\)、\(l\)、\(m\)によって決まります。
スピン量子数は、電子の分布には関係しません。
この軌道という言葉は、英語でorbitalといって、軌跡のようなものという意味になります。
電子そのものの位置は特定できず、雲のように広がっているイメージなので、ボールなどの軌跡を指すorbitとは区別されています。
電子が軌道に入るルール
ここからは、電子がそれぞれの軌道を占有するときのルールについて、お話しします。
パウリの排他原理
まず、fermi粒子はパウリの排他原理に従います。
これは、まったく同じ状態を2個以上の粒子がとることはないというルールです。
同一の原子核に拘束された複数の電子が、\(n\)、\(l\)、\(m\)、\(s\)すべてが同じ組み合わせの状態になることはありません。
フントの規則
もう1つ、フントの規則というルールがあります。
同じエネルギーの軌道が複数あるとき、電子は可能な限りスピンを平行にして異なる軌道に入ります。
図を使って説明すると、次のようになります。

まず、同じエネルギーの軌道が複数あるとき、縮退しているといいます。
縮退している2つの軌道を2個の電子が占有することを考えると、下図の左側のように片方の軌道に2個が異なるスピンをもって入るのは、エネルギー的に不利であり、右側のように1個ずつ入って、さらにスピンも同じ向きになります。
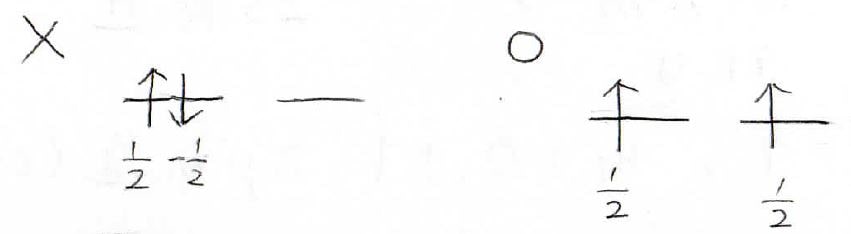
なぜこうなるかというと、まず電子は負電荷をもっているので、他の電子となるべく距離をとることで、静電反発を最小化しようとするため、別々の軌道を占有しようとします。
そして、スピンがそろうのは、量子力学的な(スピン波動関数が直交しないため、交換積分が\(\displaystyle 0\)にならず、エネルギーに差が生じる)効果として、説明されます。
\(n\)、\(l\)、\(m\)のとりうる値
ここからは\(n\)、\(l\)、\(m\)のとりうる値を考えていきます。
これまでの内容で、\(n=n’+l+1\)と\(l=|m|+k\)という2つの式が出てきていました。
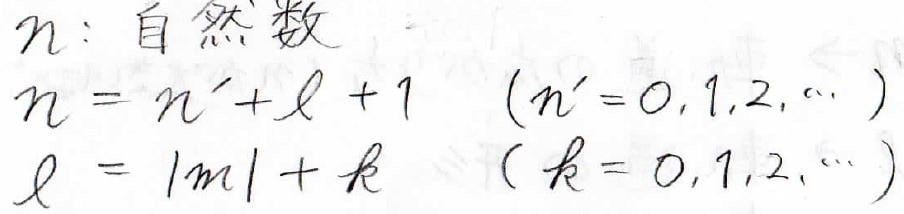
これは自然数である\(n\)を決めると、\(l\)のとりうる値が決まって、それにより\(m\)のとりうる値が決まるという関係になっています。
具体的には、このような条件になります。
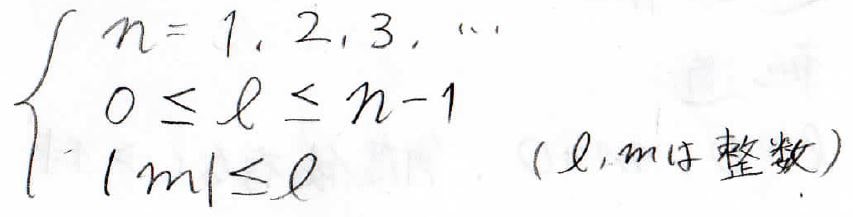
それぞれの軌道には、\(n\)と\(l\)の値に応じた名前の付け方があります。
軌道の名前を付けるときには、数字+小文字のアルファベットで表します。

数字が主量子数\(n\)で、アルファベット部分は\(l\)の値によって決まります。
\(l=0\)のときは\(\displaystyle \rm{s}\)軌道、\(1\)のときは\(\displaystyle \rm{p}\)軌道、\(2\)のときは\(\displaystyle \rm{d}\)軌道と呼びます。
\(n=1\)の場合
では、実際に\(n\)、\(l\)、\(m\)のとりうる値の例を見ていきます。
まず、\(n=1\)の場合を考えます。
\(l\)は\(0\)以上\(n-1\)以下の値をとるので、この場合は\(0\)しかとれません。
\(m\)は\(-l\)以上\(l\)以下の整数なので、これも\(0\)だけになります。
したがって、この場合は\(n=1\)、\(l=0\)なので\(\displaystyle 1\rm{s}\)軌道と呼びます。
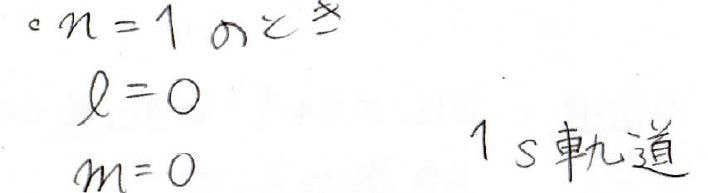
\(n=2\)の場合
\(n=2\)の場合は、\(l\)が\(0\)または\(1\)をとるので、\(\displaystyle 2\rm{s}\)軌道と\(\displaystyle 2\rm{p}\)軌道が考えられます。
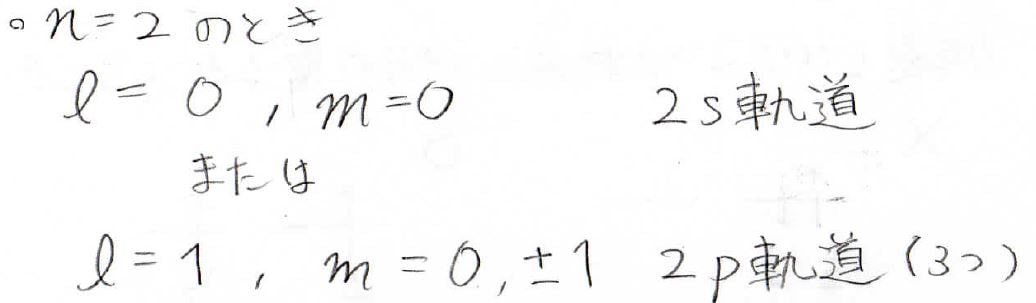
ここで、\(l=1\)のときの\(m\)は、\(0\)か\(\pm 1\)で3種類の値を取れるので、\(\displaystyle \rm{p}\)軌道は3種類存在することになります。
\(n=3\)の場合
\(n=3\)の場合は、\(\displaystyle 3\rm{s}\)軌道が1種類、\(\displaystyle 3\rm{p}\)軌道が3種類、\(\displaystyle 3\rm{d}\)軌道が5種類出てきます。

軌道の形
主量子数\(n\)は、電子がどれだけ広がるかを示す指標になっていて、大きい値ほど電子は広く分布していることになります。
方位量子数\(l\)が変わったときには、軌道の形が変わります。
磁気量子数\(m\)が変わったときに変わるのは、原則として、軌道が広がりをもつ方向だと考えてください。
\(l\)によって決まる軌道の形状は、次のようになります。
\(\displaystyle \rm{s}\)軌道の形
まず\(\displaystyle \rm{s}\)軌道は、\(l=1\)のときの球面調和関数のとおり、角度依存性がないので、球の形になります。
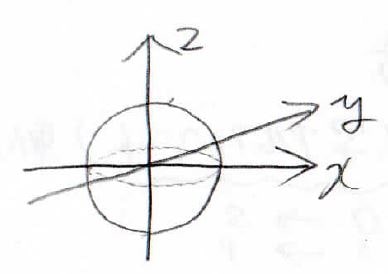
\(\displaystyle \rm{p}\)軌道の形
\(\displaystyle \rm{p}\)軌道は、下のような形になることが知られています。
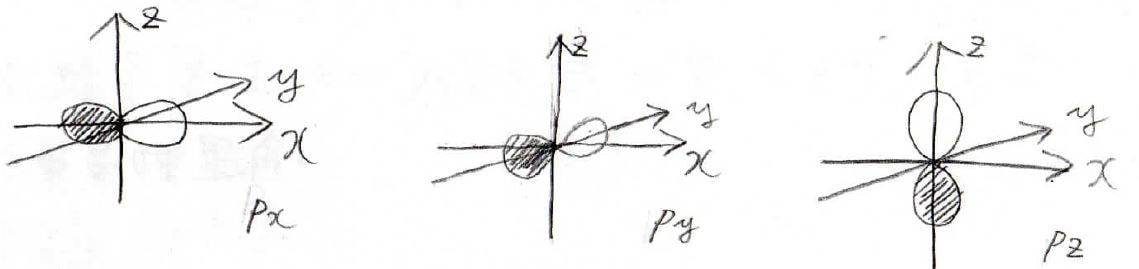
方向は\(m\)によって決まって、軌道はそれぞれの軸に平行な方向へと広がりをもちます。
上図で黒く塗った部分と白く塗った部分があるのは、これは波の位相の符号を表しています。
正弦波だと、下図のようなイメージです。
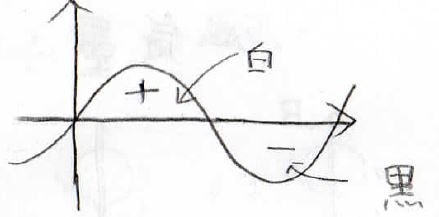
黒い部分と白い部分で、電荷の符号が違うというわけではないので、注意してください。
\(\displaystyle \rm{d}\)軌道の形
\(\displaystyle \rm{d}\)軌道については5種類あって、次のようになります。
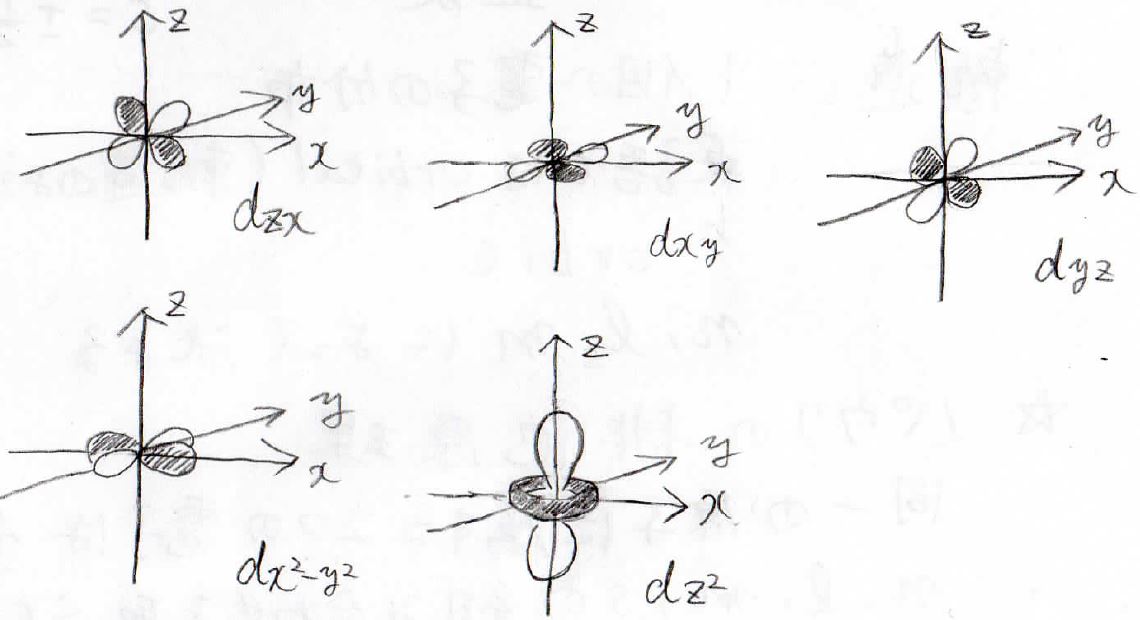
5つのうち、3つは\(x\)、\(y\)、\(z\)軸を避けるような四つ葉型になります。
そして、1つは\(x\)軸、\(y\)軸と平行になるような四つ葉型です。
5つ目は\(z\)軸に平行で、特徴的な形になります。
これら軌道の形は、錯体の物性に影響を及ぼすため、無機化学でとても重要になります。
練習問題
それでは、練習問題をしてみましょう。
Part 2の内容より
(1)\(l=0\)のとき、球面調和関数\(Y\)の角度依存性はどうなるでしょうか?
Part 3の内容より
(2)実は、シュレディンガー方程式から出たエネルギーは、ボーアの原子モデルから求めたものと一致します。
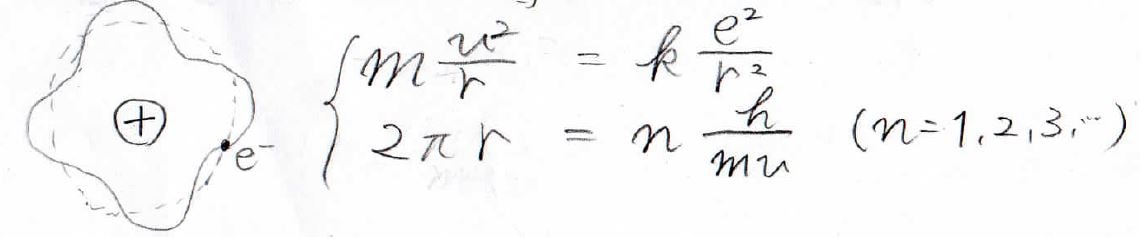
それを確かめてください。
Part 4の内容より
高校化学で習う電子殻について、K殻には電子が2個入って、L殻には電子が8個入るというルールがありました。
\(n=1\)をK殻、\(n=2\)をL殻と対応させて、量子数のとりうる値を考えれば、電子殻に入る電子の数がわかります。
ということで、内殻側から\(n\)番目の電子殻に入る電子の数が\(2n^2\)と表せることを示してください。
すると\(l=0\)なので、\(m\)は\(0\)しかとらないということになります。
次に、\(\Theta\)の式に\(m=0\)、\(l=0\)を代入してみましょう。
すると、下のように\(\Theta\)が定数になります。

これにより、\(l=0\)のときの\(\Theta\)は\(\theta\)に依存しないということになります。
\(m=0\)のときは\(\Phi\)も定数になるため、\(\varphi\)にも依存しなくなります。
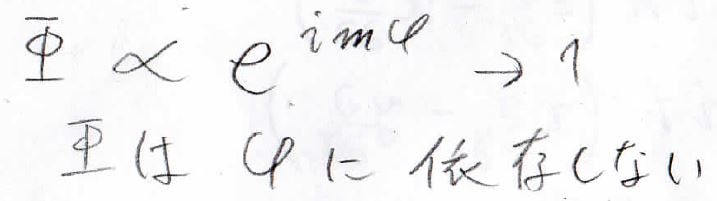
したがって\(l=0\)のとき、\(Y\)は定数となって\(\theta\)にも\(\phi\)にも依存しないということになります。
このときは、波動関数が原子核からの距離\(r\)のみの関数となって方向性をもたないので、球状に電子が分布することになります。
(2)ボーアの原子モデルの連立方程式を解くと、回転半径\(r\)と速さ\(v\)が求まります。
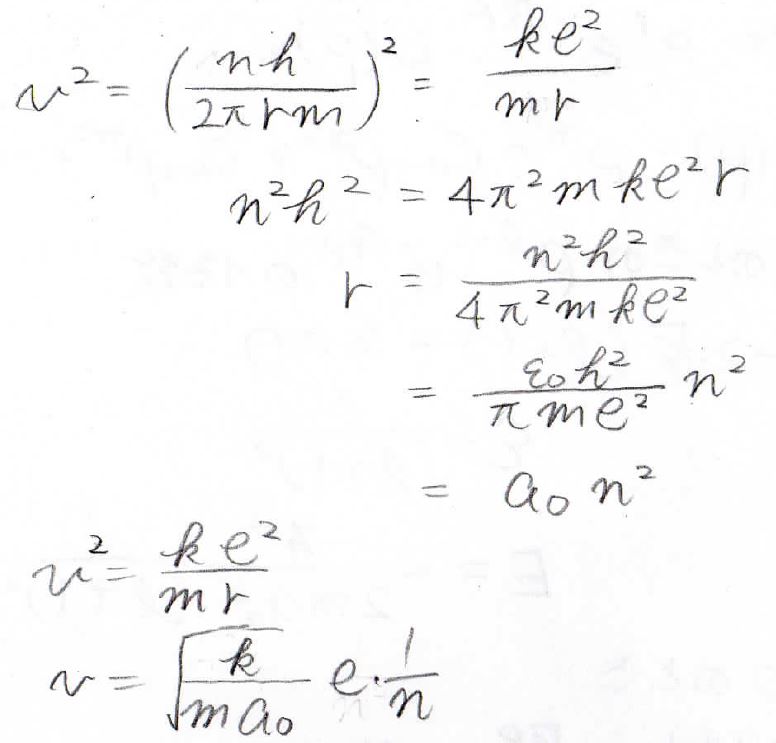
これを全エネルギーの式に代入すると、エネルギーが\(\displaystyle -\frac{ke^2}{2a_0}\frac{1}{n^2}\)となります。
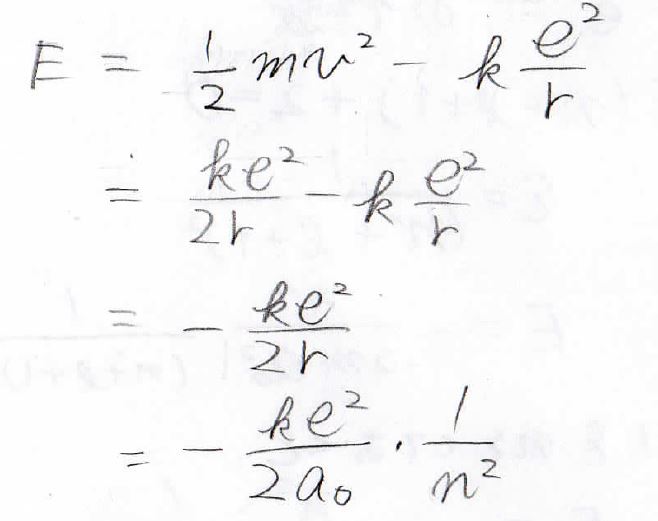
これがシュレディンガー方程式の答えと一致することを示すには、その比をとって\(1\)であることを証明すればよいので、比を計算すると、\(\displaystyle \frac{kme^2}{\hbar ^2}a_0\)となります。
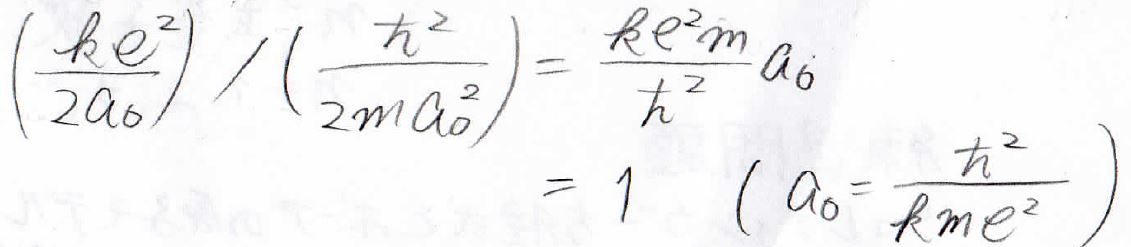
\(\displaystyle a_0=\frac{\hbar ^2}{kme^2}\)を代入すると、この値は\(1\)になるので、シュレディンガー方程式から計算したエネルギーと、ボーアのモデルから計算したエネルギーは、たまたまですが、一致することになります。
ボーアのモデルは、量子の波動性を考えながら古典力学を使うという強引なモデルなのですが、水素様原子のエネルギーに関しては、正しい値が出ます。
(3)とりうる\(l\)の値は\(n-1\)個になって、さらにそれぞれの\(l\)について、\(m\)は\(2l+1\)個の値をとれます。
その総数は\(\sum\)を使って、このように書けます。
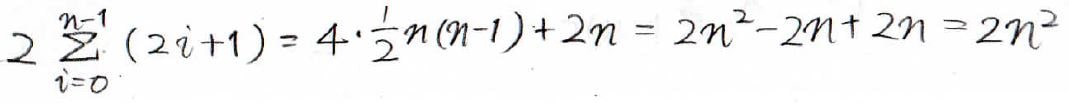
スピンを考慮しているので、\(2\)がかかっています。
この級数の和を求めると、\(2n^2\)となります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!