こんにちは!
今日も数学の話をやっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(jacobian)
では早速内容に入っていきます。
重積分とは
重積分とは、以下のように多変数関数を複数の変数について積分するという演算のことです。
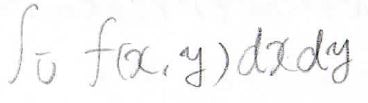
ここでは二重積分を例としていて、積分の範囲は\(xy\)平面上の\(\bar{U}\)という領域になります。
\(\bar{U}\)は有界な領域であり、この領域上で連続な関数\(f(x,y)\)について、積分を考えています。

ここで、有界を簡単に言うと閉じているということです。
定義に近い言い回しをすると、\(\bar{U}\)を完全に含むような領域\(\bar{V}\)が存在するときに、\(\bar{U}\)は有界であるといいます。
そして、リーマン和の考え方より、領域\(\bar{U}\)での重積分というのは、まず\(\bar{U}\)を小さく分割していって、高さを\(f(x,y)\)とする立体の体積の和として考えることができます。
この考え方により、\(\bar{U}\)が下のような複雑な形でも単純化できます。
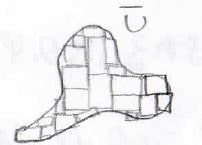
重積分の計算方法
ここからは、実際の計算方法の話をしていきます。
長方形の領域上での重積分
まず、長方形の領域について、重積分を考えます。
ここで、\(f(x, y)\)は領域\(\bar{U}\)上で連続な関数であるとします。
領域\(\bar{U}\)は\(x\)が\(a\)から\(b\)まで、\(y\)が\(c\)から\(d\)までとします。

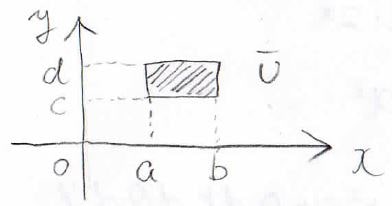
\([]\)は閉区間、すなわち端の値も含めるという意味です。
\(()\)は開区間で、端の値を含みません。
そして、そのときの重積分はこうなります。
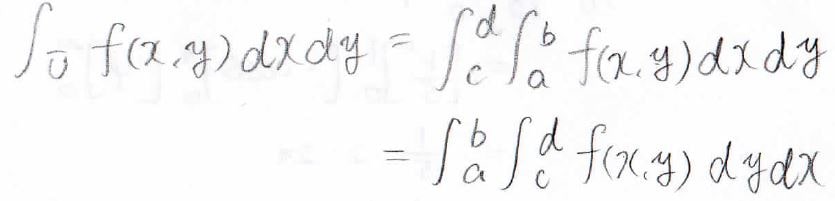
2つの変数についての積分ですが、まずは\(y\)を定数とみなして、\(x\)について一変数関数の積分をします。
そうすると、\(x\)が消えて\(y\)だけの関数になるので、そのあとで\(y\)について積分します。
この\(x\)と\(y\)の順番は、交換しても同じ値になります。
ただし、積分領域に変数が入っている場合は例外です。
\(y\)の範囲が\(x\)の関数の領域上での重積分
続いて、\(y\)の範囲が\(x\)の関数によって決められている場合を考えてみます。
領域\(\bar{U}\)は、下のようなイメージです。
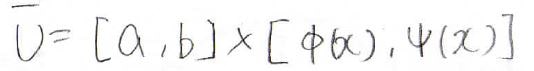
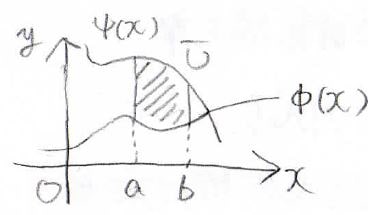
2つの関数\(y=\phi (x)\)と\(y=\psi (x)\)、そして\(x=a\)と\(x=b\)という2本の直線によって囲まれた領域が\(\bar{U}\)です。
このときの重積分は、まず\(x\)を固定して、\(y\)の範囲を関数そのまま入れます。
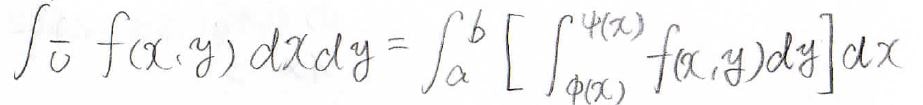
すると、\(y\)が消えて\(x\)だけの関数になるので、そのあとで\(x\)について積分します。
例えば、円の面積が\(\pi r^2\)で与えられることは、以下のようにして導くことができます。
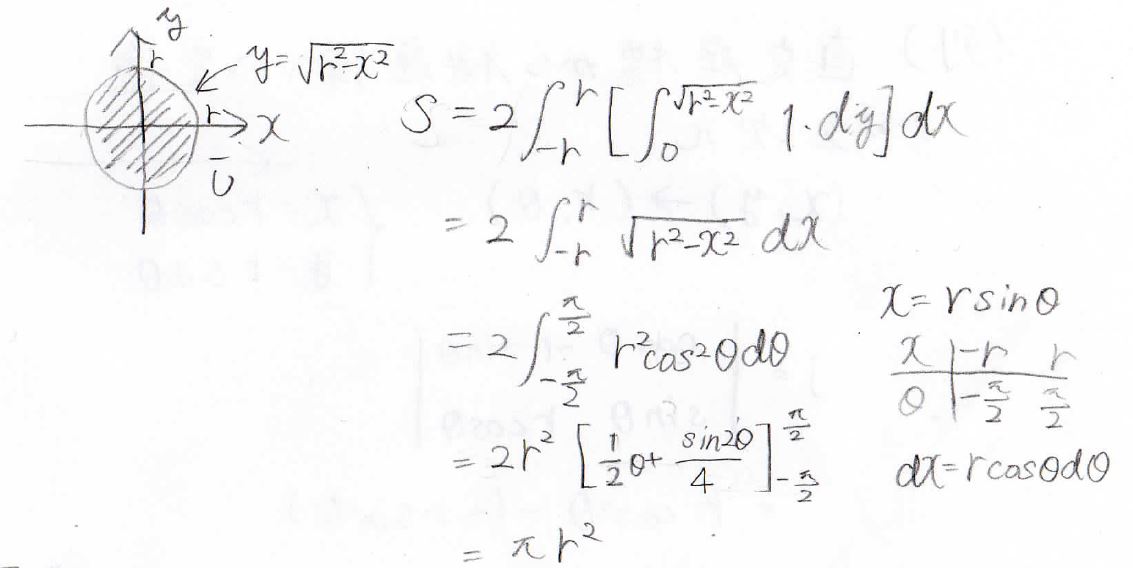
円の式は\(x^2+y^2=r^2\)で、これを\(y\)について解くと、\(\pm \sqrt{(r^2-x^2)}\)になります。
半円の面積を2倍にすることを考えると、円の面積\(S\)は上の形で与えられます。
ここで、\(1\)は高さだと思ってください。
この領域の面積は、この領域を底面とする高さ\(1\)の円柱の体積と等しい値となります。
あとは順番通り計算していくことで、円の面積の公式を導くことができます。
置換積分
それでは今度、置換積分を考えます。
置換積分とは、一変数の積分だとこういうものです。
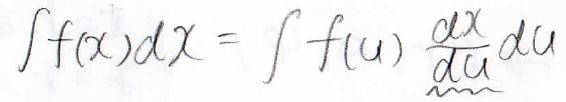
\(x\)と異なる変数を使ったほうが計算が簡単になる場合に、置換積分をします。
その際、変換前後のそれぞれの微小変化量の比は、微分によって求められ、積分の式の中に残ってきます。
この記事では、この波線を引いた部分が多変数関数だとどうなるのかというのを考えていきます。
まずは、いちばん簡単な二変数の置換積分を考えます。
多変数での微小変化量の前につく値がどうなるのか、結論を先にいいますと、こちらの式になります。
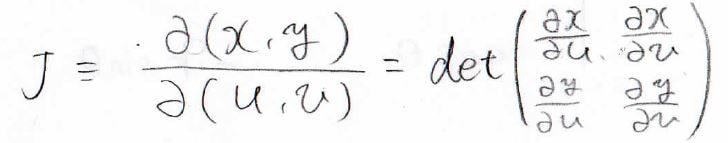
まず、\(x\)と\(y\)を移し先の変数である\(u\)と\(v\)で微分します。
そして、それらを行列として書いて、その行列式こそが、波線部のものと同等になります。
この行列式のことをヤコビアンと呼びます。
二次元空間におけるヤコビアンは、微小面積である\(\rm{d}\)\(u\rm{d}\)\(v\)を基準にどれだけ大きくなれば\(\rm{d}\)\(x\rm{d}\)\(y\)になるのかという値です。
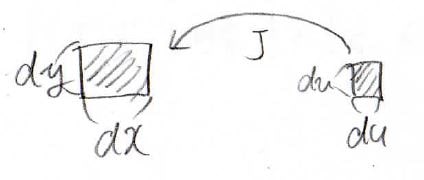
以前の記事の中で、\(2\)次行列式は2つのベクトルで貼られる平行四辺形の面積になるという話をしましたが、これと同じイメージです。
行列式と幾何の問題との関係については、こちらをご覧ください。

当然ですが、変数の数が増えた場合には、それだけ考えられる偏導関数が増えるため、ヤコビアンは\(N\)次行列式になります。
直交座標から極座標への変換
ヤコビアンの例として、直交座標から極座標への変換の場合を考えてみましょう。
2次元
まず、2次元について考えます。

\(x\)と\(y\)を\(r\)と\(\theta\)で表した式より、ヤコビアンは下のようになり、最終的に\(r\)となりました。
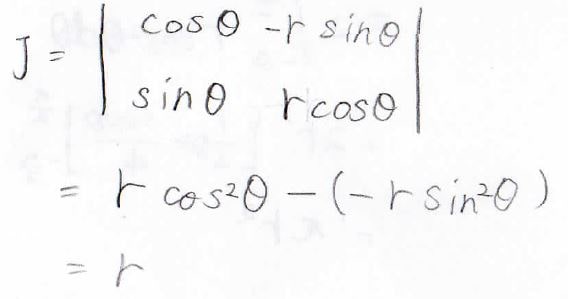
直交系の二変数関数を極座標にして積分する際には、\(r\)をつけ忘れないようにしましょう。
3次元
3次元の場合、行列式をサラスの方法によって解くと、\(r^2\sin{\theta}\)となります。

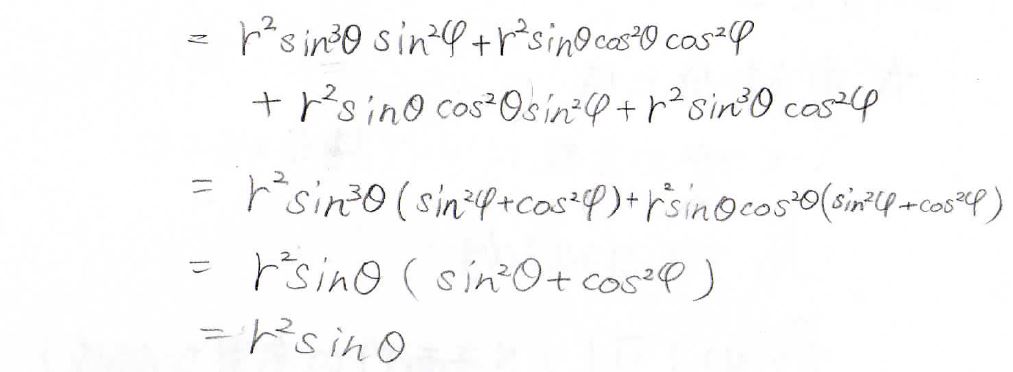
この結果は、自然科学で頻繁に使われます。
低次の行列式の解き方については、こちらをご覧ください。

練習問題
最後に、練習問題をやってみましょう。
(1)半径が\(a\)の球の体積が\(\displaystyle \frac{4}{3}\pi a^3\)で与えられることを重積分から導いてください。
(2)半径が\(1\)の球という領域について\(x^2+y^2+z^2\)を積分すると?


球の中の無限に小さい点を数え上げるようなイメージ、もしくは球を玉ねぎ状に厚さが\(a\)になるまで重ねたときの表面積の和と考えてもいいです。
こうすることで、球の体積の公式を導くことができました。
そして(2)は、式に当てはめることで解くことができて、その答えは\(\displaystyle \frac{4}{5}\pi\)になります。
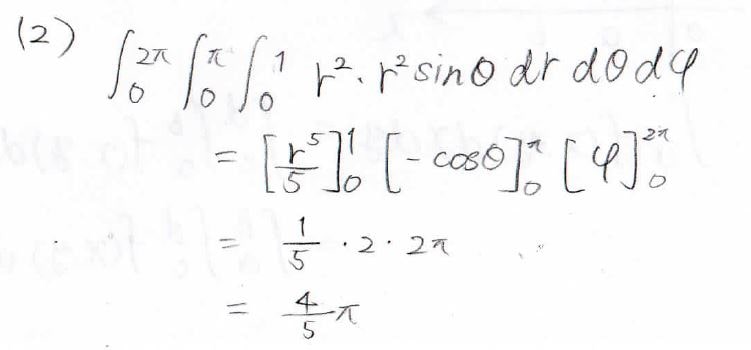
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




