こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマは、こちら!
動画はこちら↓
動画で使ったシートはこちら(Carnot cycle)
それでは内容に入っていきます!
熱機関とは?
熱機関とは、熱を与えることで、外部へ仕事をする装置のことです。
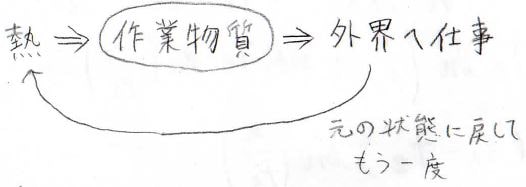
さらに、1回しか仕事をしてくれないものだと、非効率なので、繰り返し仕事が行えるように再度元に戻れる仕組みを組み込みます。
ここで、作業物質は理想気体とし、可逆系を考えることとします。
熱機関の例
では、ここで熱機関の例を見ていきましょう。
カルノー(Carnot)サイクル
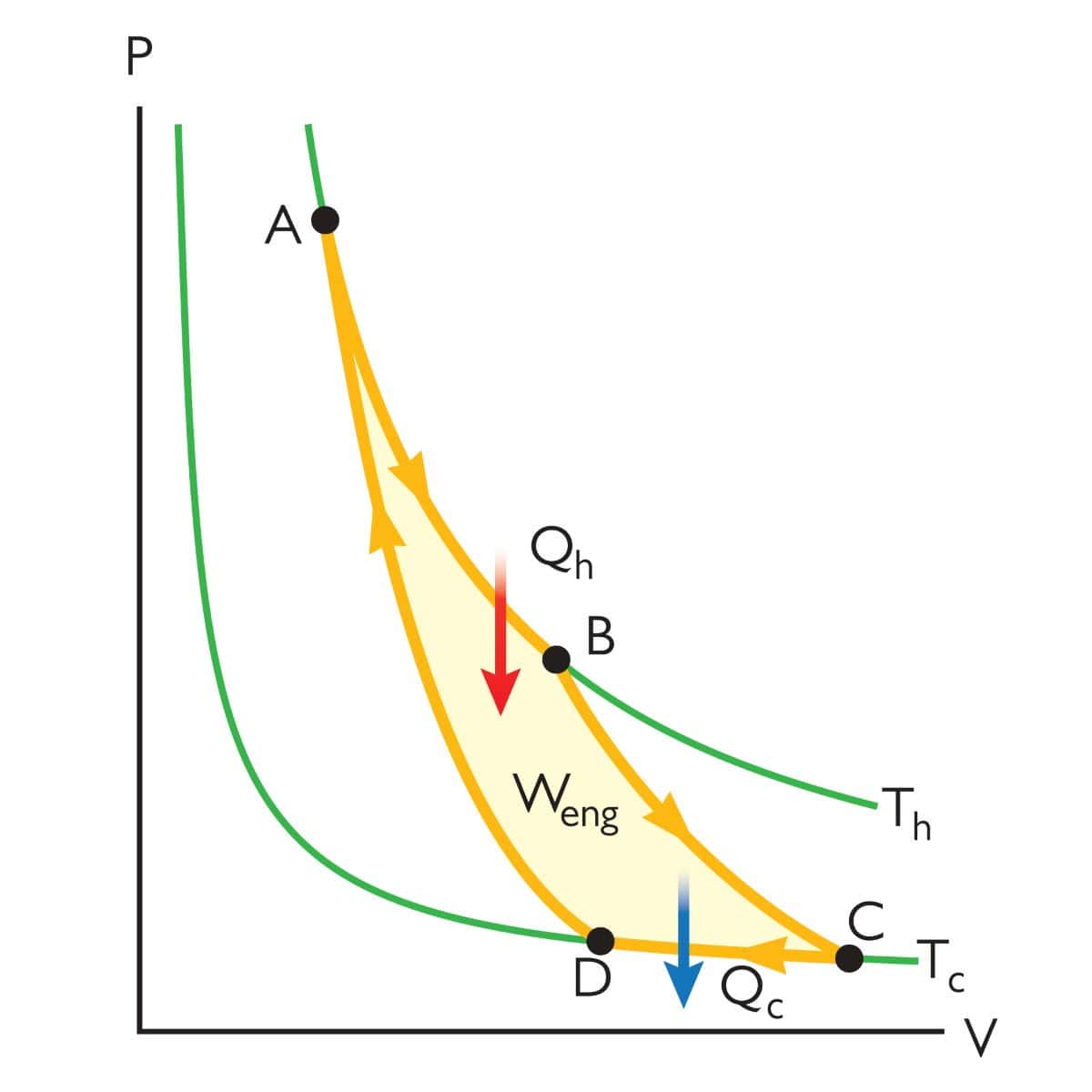
まず、最も基本的なカルノーサイクル。
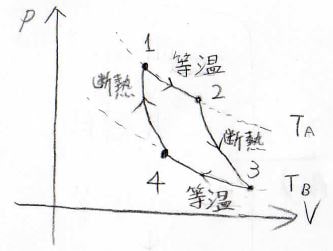
2つの等温変化と2つの断熱変化で1周するサイクルです。
1周した後は、再度同じように仕事をすることができます。
カルノーサイクルについては、この後の話で、もう少し深堀していきます。
オットー(Otto)サイクル
そして、次の熱機関の例は、オットーサイクルです。
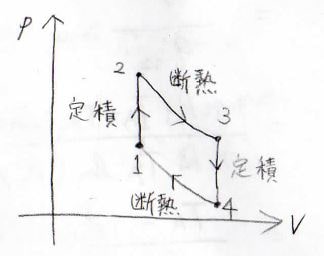
これは、2つの定積変化と2つの断熱変化で1周するサイクルです。
ガソリンエンジンやガスエンジンンの理論サイクルになります。
ディーゼル(Diesel)サイクル
3つ目の例は、ディーゼルサイクルです。

定積変化と定圧変化が1つずつと2つの断熱変化で1周します。
名前のとおり、ディーゼルエンジンの理論サイクルです。
ブレイトン(Brayton)サイクル
そして、最後に紹介する例は、ブレイトンサイクルです。
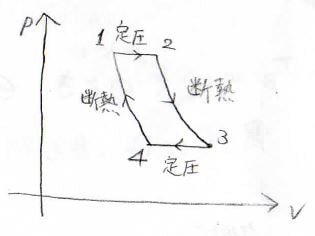
2つの定圧変化と2つの断熱変化で1周し、ガスタービンやジェットエンジンの理論サイクルとして知られています。
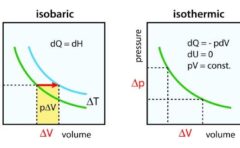
なお、定積変化と定圧変化については、こちらの記事で詳しく解説しています。
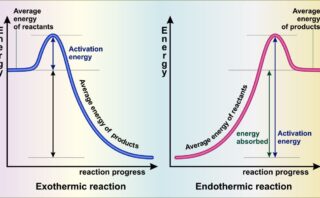
等温変化、断熱変化については、こちらです。
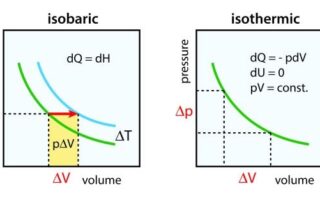
これらの共通点
これらは共通して、\(p\)-\(V\)グラフ上で時計回りに1周しており、その閉じられた領域の面積が、外界へされた仕事に等しくなります。
また、4つの変化から構成されており、そのうちの2つは断熱変化です。
そして、熱を受け取る過程は4つのうちの1つだけになります。
カルノーサイクルにおける仕事と熱
ここからは、カルノーサイクルについて詳しく見ていきましょう。
\(p\)-\(V\)グラフ上で最も左上の点を\(1\)として、下記のように番号を付けることにします。
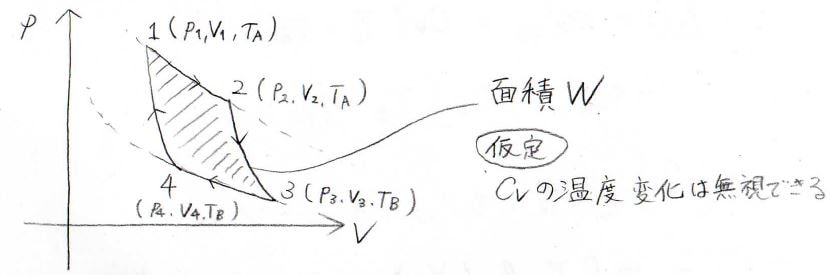
それぞれのときの状態量は、この番号を添え字にして表すことにします。
そして、状態\(1\)と状態\(2\)、状態\(3\)と状態\(4\)は温度が等しくなるので、前者の温度を\(T_\rm{A}\)、後者の温度を\(T_\rm{B}\)と表すことにします。
閉じられた領域の面積は\(W\)とし、この変化の途中で定積熱容量\(C_V\)の温度変化は無視できるものとします。
熱容量の温度依存性については、こちらを参照してください。

1周のサイクルで系が外部へした仕事\(-w\)は面積\(W\)に等しく、また各過程における仕事の和と考えることができるので、ここからはそれぞれの変化について考えていきます。
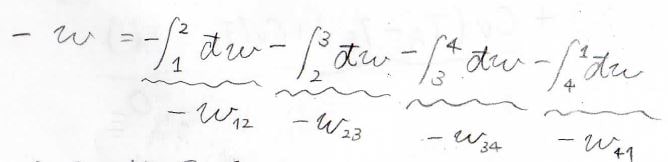
等温膨張(\(1\)→\(2\))
まずは状態\(1\)から\(2\)への等温膨張です。
系に与えられた微小な仕事\(\rm{d’}\)\(w\)は\(-p\rm{d}\)\(V\)で与えられ、理想気体の状態方程式より\(\displaystyle p=\frac{nRT}{V}\)となるため、外部への仕事\(-w\)は\(nRT_\rm{A}\)\(\displaystyle \ln(\frac{V_2}{V_1})\)と求められます。
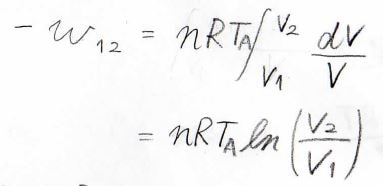
また、温度変化がないとき、理想気体の内部エネルギーは一定になるので、熱力学第一法則より系に与えられた熱量\(q\)は\(-w\)になります。

体積\(V_1\)と\(V_2\)を比べると、\(V_2\)の方が大きいので、\(q\)は正の値となります。
熱力学第一法則については、こちらを参照してください。
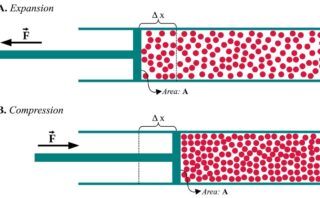
断熱膨張(\(2\)→\(3\))
続いて、状態\(2\)から\(3\)への断熱膨張について考えてみます。
系へされた仕事\(w\)は、内部エネルギーの変化量と等しく、\(C_V(T_\rm{B}\)\(-T_\rm{A})\)となります。
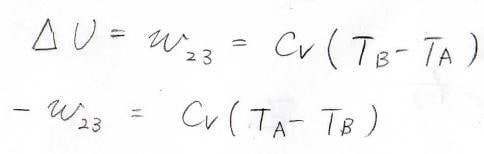
もちろん、外部へ正の仕事をしているので、\(w\)は負の値になります。
等温圧縮(\(3\)→\(4\))
そして、状態\(3\)から\(4\)までの等温圧縮では、先ほどと同様の考え方で、\(-w\)が\(nRT_\rm{B}\)\(\displaystyle \ln{(\frac{V_4}{V_3})}\)となります。
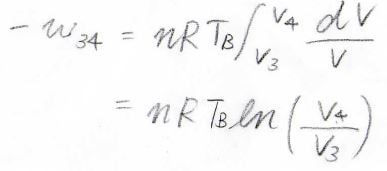
系に与えられた熱量\(q\)も同じ値となり、\(V_4\)は\(V_3\)より小さいので、\(q\)は負の値となります。
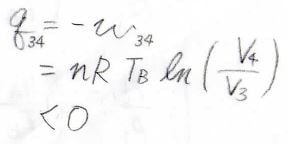
つまり、この過程では、熱を外部へ放出していることになります。
断熱圧縮(\(4\)→\(1\))
そして最後、状態\(4\)から\(1\)までの変化では、\(w\)が\(C_V(T_\rm{A}\)\(-T_\rm{B})\)となり、これは正の値となります。
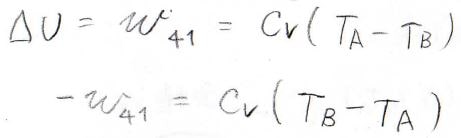
サイクル全体
全体を通してみると、系が外部へした実質の仕事は、断熱過程の値がキャンセルして、結局\(nRT_\rm{A}\)\(\displaystyle \ln{(\frac{V_2}{V_1})}+nRT_\rm{B}\)\(\displaystyle \ln{(\frac{V_4}{V_3})}\)となります。
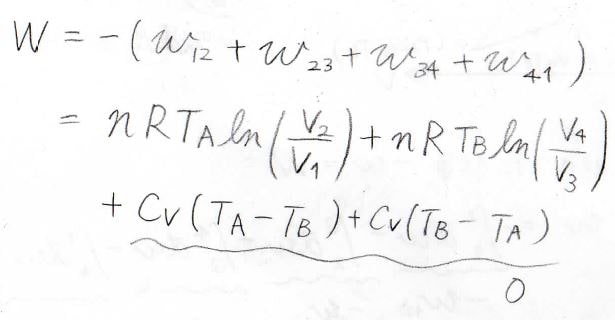
ここで、断熱変化で成り立つPoissonの式を思い出してみると、理想気体の状態方程式より、\(\displaystyle pT^\frac{\gamma}{1-\gamma}\)が一定となるので、状態\(2\)と\(3\)、状態\(4\)と\(1\)で、圧力と温度の関係式は、下のようになります。

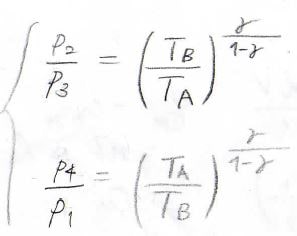
したがって、圧力の比には、\(\displaystyle \frac{p_2}{p_3}=\frac{p_1}{p_4}\)という関係が成り立ちます。
また、理想気体であれば、\(\displaystyle \frac{V_2}{V_1}=\frac{p_1}{p_2}\)が成り立つため、\(\displaystyle \frac{V_4}{V_3}=\frac{p_3}{p_4}=\frac{p_2}{p_1}\)となります。

したがって、\(W=nR(T_\rm{A}\)\(-T_\rm{B}\)\(\displaystyle )\ln{(\frac{p_1}{p_2})}\)という形に変形することができます。
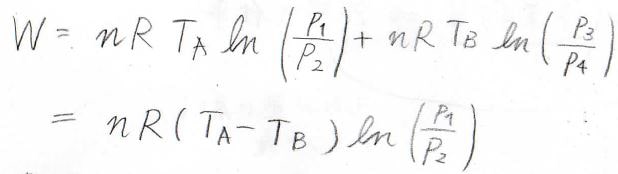
\(T_\rm{A}\)は\(T_\rm{B}\)より大きく、\(p_1\)は\(p_2\)より大きいため、\(W\)は必ず正の値となることがわかります。
熱効率
最後に、カルノーサイクルの熱効率について考えてみましょう。
熱効率とは、系に与えた熱のうち、どれくらいが仕事に変換されるのかという割合で、\(0\)から\(1\)までの値をとります。
系へ熱が与えられるのは、状態\(1\)から\(2\)までの等温膨張過程だけであり、熱効率\(e\)は、このように導かれます。

分母と分子に共通して\(nR\ln{(p_2/p_1)}\)があるので、これを消すと、\(\displaystyle \frac{T_\rm{A}-\mathit{T}_\rm{B}}{T_\rm{A}}\)となり、温度だけで表されることになります。
これは\(\displaystyle 1-\frac{T_\rm{B}}{T_\rm{A}}\)とも書けるため、これら2つの温度が近い値のときには効率が悪く、離れているほど効率が良いことになります。
熱効率は、\(1\)にできない?
\(T_\rm{B}\)を\(0\ \rm{K}\)にすれば、熱効率を\(1\)にすることができますが、実際に有限の温度をもつ物質を絶対零度まで冷やす手段はないので、熱効率は必ず\(1\)より小さい値となります。
実は、与えられた熱をすべて仕事に変換することはできなくて、一部は熱として捨てる必要があります。
これはKelvinの原理と呼ばれるもので、熱力学第二法則の表現の1つです。
詳しくは、こちらの記事をご覧ください。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!