こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
それでは内容に入っていきます!
ヒュッケル法で何がしたいのか
まず、今回お話しするヒュッケル法で何がしたいのかということから始めていきます。
それはずばり、\(\displaystyle \pi\)電子が非局在化したときのエネルギー準位をなるべく簡単に求めるということです。

有機化学で共鳴安定化とよく言いますが、なぜ安定化するのか、どのくらい安定化するのかを、このヒュッケル法で考えることができます。
共鳴安定化についてはこちらの記事でもお話ししています。
今回はヒュッケル法の理論の話なので、少し難しいかもしれませんが、かみ砕いて説明していきます!
まず、炭素鎖上の\(\pi\)電子のうち、1個が\(i\)番目の状態にあったとします。
その波動関数\(\phi_i\)を炭素原子の原子軌道の線形結合で書けると考えます。
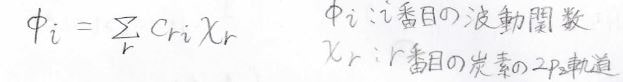
これはLCAO(Linear Combination of Atomic Orbital)近似と言います。
さらに、今度は分子中に存在するすべての\(\displaystyle \pi\)電子について考えます。
\(n\)個の電子の並べ方は\(n!\)通りありますが、その中の1つを\(j\)と表すことにします。
その\(j\)という並べ方において、\(i\)番目の電子が属するエネルギー状態の波動関数を\(\phi_{N_i, j}\)とすると、\(j\)という電子の並べ方をしたときの波動関数\(\psi_j\)はこのようになります。
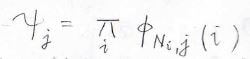
考えうるすべての状態の寄与を考えたものを全体の波動関数\(\Psi\)とすると、下のようになります。
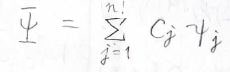
そして、fermi粒子である電子はパウリの排他原理に従うため、この波動関数は反対称性を満たさなければいけません。
そんな条件を満たす\(\Psi\)を表すのにとっておきの方法は、行列式で表記するということです。

この行列式は、スレーター行列式と言います。
行列式には同じ行が存在すると\(0\)になる、すなわち規格化条件を満たさなくなったり、行の入れ替えによって符号が入れ替わることで反対称性を表現できたりする性質があります。
詳しくはこちらの記事でお話ししています。

シュレディンガー方程式の変形
こうして行列式で書かれた波動関数を使い、エネルギー準位を求めていきます。
とは言っても、多体問題であるために厳密に解くことはできないので、さらなる仮定が必要です。
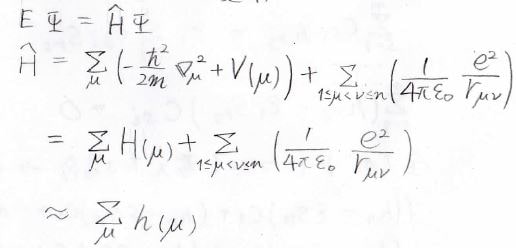
ハミルトニアンの静電ポテンシャルを表す項がこの問題を複雑にしているので、全体のハミルトニアンが個々の電子のハミルトニアン\(h(\mu)\)に分離できるものと仮定します。
すると、\(\mu\)番の電子についてのシュレディンガー方程式が書けます。
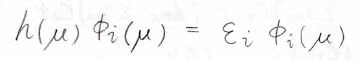
ここで\(\varepsilon_i\)は\(i\)番目の状態のエネルギーです。
これを求めると、こうなります。

ここで\(h_{rs}\)は\(r\)と\(s\)が同じときはクーロン積分、異なるときは共鳴積分に対応するエネルギーの安定化を表します。
\(S_{rs}\)は重なり積分です。
ここに関しては、こちらの記事の後半部分でもお話ししています。
右辺の分母を両辺にかけて分数をなくすと、下の形になります。

ここで\(r\)を固定して、ある1つの\(C_{ri}^\ast\)で両辺を偏微分します。
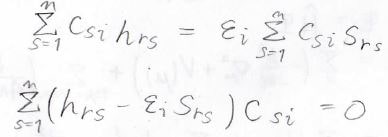
すると、両辺を\(C_{si}\)でくくれるようになります。
すべての\(r\)について考えた場合には、このような式が\(n\)個出てくることになり、下のような連立方程式ができます。
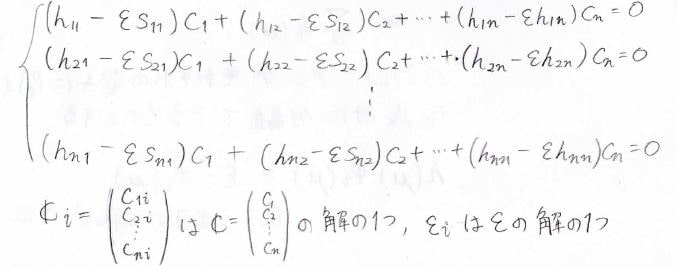
この連立方程式は永年方程式と呼びます。
ここで\(\boldsymbol{C}_i\)は係数の列ベクトル\(\boldsymbol{C}\)の解の1つ、\(\varepsilon_i\)は状態エネルギー\(\varepsilon\)の解の1つです。
ここで、\(\boldsymbol{C}=\boldsymbol{0}\)という解が存在していますが、もしすべての係数が\(0\)だった場合には、波動関数が\(0\)ということになり、規格化条件を満たしません。
そのような解以外にも右辺がすべて\(0\)となる解をもっているということなので、この永年方程式の係数行列は正則行列ではないことになります。
したがって、係数行列の行列式は\(0\)になります。
詳しい説明はこちらの記事をご覧ください。

ヒュッケル近似
それでは実際にこの連立方程式を解いていきます。
ここでもさらに近似を入れて、なるべく簡単に解けるようにします。
隣接する炭素からの影響しか考えないという考え方で、この近似はヒュッケル近似と言います。

これを使うと、末端以外はすべて下の式で表せることになります。
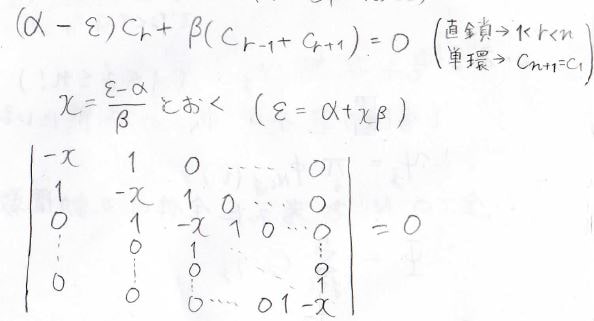
単環状分子では連立方程式のすべての式がこの式になります。
ここで、\(x\)を\(\displaystyle \frac{\varepsilon-\alpha}{\beta}\)とすると、もっと式を簡単にできます。
結局、解くべき行列式は\(0\)と\(1\)と\(-x\)しか出てこない、単純なものになります。
連立方程式の\(x\)の解がわかれば、状態エネルギー\(\varepsilon=\alpha+x\beta\)より、エネルギー準位を求めることができます。
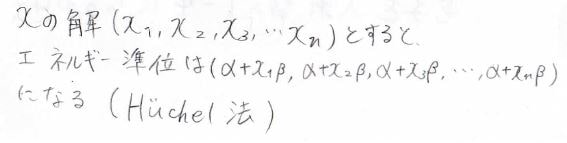
このようにして\(\displaystyle \pi\)電子のエネルギー準位を求める方法こそがヒュッケル法です。
実際の計算例は、こちらの記事をご覧ください。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




