こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(contribution to molecular partition function)
それでは内容に入っていきます!
分配関数の定義
始めに、分配関数の定義のおさらいをします。
分子分配関数は、ボルツマン分布の式についてお話ししたとき、全体の分子数を考えるのに便利な量として紹介しました。
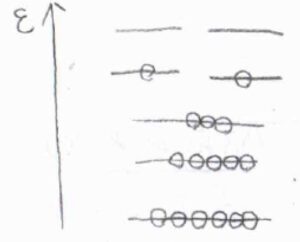
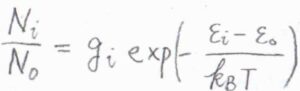
詳しくは、こちらを参照してください。

その定義は、すべての状態について、\(\displaystyle \exp{(-\frac{\varepsilon_i-\varepsilon_0}{k_\rm{B}\mathit{T}})}\)の和をとるというものです。

\(\varepsilon_i\)は\(i\)番目のエネルギー準位、\(k_\rm{B}\)はボルツマン定数、\(T\)は絶対温度です。
すべての状態について考えるため、縮退している場合は、縮退度\(g_i\)が付きます。
温度が低いときには、高いエネルギーをもつ状態に分子は存在しにくくなり、分子分配関数は小さくなります。
高温極限では分子分配関数は無限大となり、絶対零度近傍では基底状態の縮退度と等しくなります。
したがって、分子分配関数は、熱的に励起可能な状態の数であると考えることができます。
これは、あくまで1つの分子の状態から考えた結果ですが、多数の分子が存在している正準アンサンブルについても、各状態のエネルギーから集合分配関数\(Q\)が定義されます。
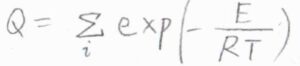
ここで、\(\displaystyle E\)は絶対零度におけるエネルギーを基準とした系全体のエネルギーで、分子間相互作用も考慮されたものです。
仮に、系に含まれる分子がすべて同じで、分子間相互作用もないとき、分子分配関数と集合分配関数の関係は、\(\displaystyle Q=\frac{q^N}{N!}\)で与えられます。
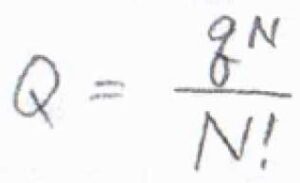
ここで、\(N\)は全分子数です。
分子分配関数の内訳
ここからが新しい内容です。
この記事では、分子がもつエネルギーを並進、回転、振動、電子の自由度に振り分けることを考えます。
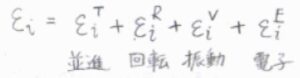
ただし実際には、並進はさておき、それぞれの自由度は完全に独立ではなく、電子状態の遷移によって振動特性が変化したり、振動状態によって回転定数が変化したりします。
詳しくは、こちらの記事を参照してください。


ここでは、多くの物質で電子遷移のエネルギー差が比較的大きいことから、電子状態は常に基底状態にあり、ボルン-オッペンハイマー近似が適用できる分子を仮定しています。
また、回転定数も振動状態に依存しないものとします。
こうして分離されたエネルギーから分子分配関数を考えると、指数同士の足し算を掛け算へと書き換えることで、それぞれの運動についての分配関数の積として因数分解することができます。
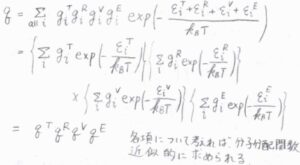
このことより、それぞれの寄与がわかれば、分子分配関数を近似的に求めることができます。
ということで、ここからは、それぞれの分配関数を順番に考えていきます。
電子分配関数
始めに、最も簡単である電子状態について考えます。
先ほども述べたとおり、基底状態からの励起に必要なエネルギーは、並進や回転や振動に比べてきわめて大きく、すべての分子が電子基底状態にあるとしても、分配関数の議論には大きな問題が起こらないことが多いです。
そのとき、電子分配関数は、基底状態の縮退度に等しく、多くの分子について、\(1\)となります。
ただし例外もあり、たとえば一酸化窒素の基底状態と第一励起状態のエネルギー差は、スピン-軌道カップリングによるもので、波数で\(121\ \rm{cm}\)\(^{-1}\)という小さな値をもちます。
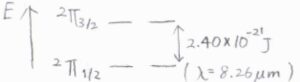
このような場合には、第一励起状態も励起可能な状態に数えられます。
一酸化窒素について、このエネルギー差を\(\varepsilon\)としたとき、電子分配関数は\(\displaystyle 2+2\exp{(-\frac{\varepsilon}{k_\rm{B}\mathit{T}})}\)となります。
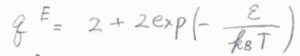
縦軸を分配関数、横軸を絶対温度としてグラフを書くと、こちらのようになります。

温度が\(\displaystyle \frac{\varepsilon}{k_\rm{B}}\)、すなわち\(149\ \rm{K}\)よりもはるかに小さければ、分配関数は第一励起状態の縮退度\(2\)と等しくなりますが、高温では第一励起状態の縮退度も含めた\(4\)に収束します。
スピン分配関数
これは余談ですが、電子のスピン状態についても分配関数を考えることがあるので、少しお話しします。
外部磁場\(\boldsymbol{B}\)のもとにある電子は、スピンの配向によって、2つのエネルギー状態をとることが知られています。
これをゼーマン効果と言います。
スピン量子数を\(m_\rm{s}\)として、各状態のエネルギー\(E\)は、\(2\mu_\rm{B}\)\(Bm_\rm{s}\)で与えられます。
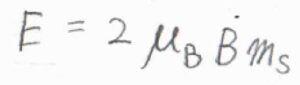
ここで、\(\mu_\rm{B}\)はボーア磁子です。
電子についての\(g\)因子を簡単に\(2\)と考えています。
状態間のエネルギー差は\(2\mu_\rm{B}\)\(B\)であるため、スピン分配関数は\(\displaystyle 1+\exp{(-\frac{2\mu_\rm{B}\mathit{B}}{k_\rm{B}\mathit{T}})}\)と書けます。
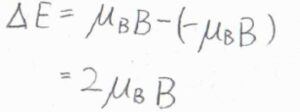
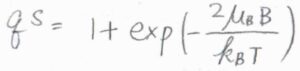
並進分配関数
それでは、本題に戻って、並進運動についての分配関数を考えていきます。
一次元並進運動の寄与
始めに、大きさが\(X\)の一次元の箱の中に、質量\(m\)の分子が1つある系を考えます。
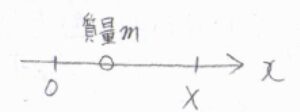
一次元井戸型ポテンシャルのエネルギー準位は、\(n\)を自然数として、\(\displaystyle E_n=\frac{n^2h^2}{8mX^2}\)となります。

ここで、\(h\)はプランク定数です。
導出の過程は、こちらを参照してください。

基底状態のエネルギー\(\displaystyle \frac{h^2}{8mX^2}\)を\(\varepsilon\)として、これを基準にしたエネルギーを\(\varepsilon_n\)とすると、\(\varepsilon_n=(n^2-1)\varepsilon\)と書けます。
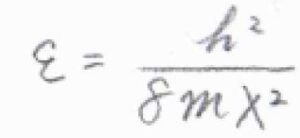
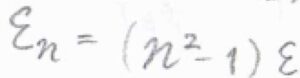
したがって、並進分配関数は、\(\displaystyle \sum^\infty_{n=1}\exp{[-\frac{n^2-1}{k_\rm{B}\mathit{T}}\varepsilon]}\)となります。
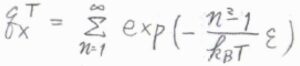
さらに、実験室で一般的に使われている容器のサイズだと、並進運動のエネルギー準位の間隔がきわめて小さいです。
エネルギーを連続関数と近似することで、より簡単に分配関数を表すことができます。

このとき、積分範囲の下限を\(n=1\)から\(n=0\)にすると同時に、\(n^2-1\approx n^2\)と近似しても、大きな誤差は生じません。
\(\displaystyle x^2=\frac{n^2\varepsilon}{k_\rm{B}\mathit{T}}\)とおいて置換積分すると、\(q^\rm{T}\)\(\displaystyle =\sqrt{\frac{\pi k_\rm{B}\mathit{T}}{4\mathit{\varepsilon}}}\)となります。
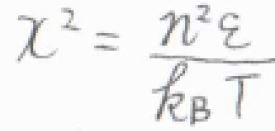
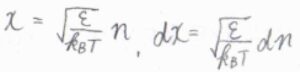
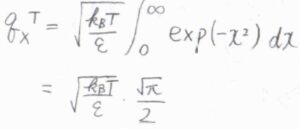
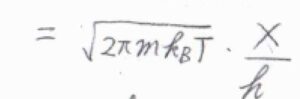
\(\displaystyle \varepsilon=\frac{h^2}{8mX^2}\)を代入すると、\(q^\rm{T}\)\(\displaystyle =\sqrt{2\pi mk_\rm{B}\mathit{T}}\frac{X}{h}\)となります。
したがって、並進分配関数は箱の大きさに比例することになります。
その比例定数の逆数である\(\displaystyle \frac{h}{\sqrt{2\pi mk_\rm{B}\mathit{T}}}\)は、長さの次元をもつパラメータで、熱波長もしくは熱的ド・ブロイ波長と呼ばれます。

ここでは、熱波長を\(\Lambda\)と表します。
粒子の質量が大きくなったり、温度が上昇したりすると、\(\Lambda\)は小さくなり、並進分配関数は大きくなります。
これは、並進のエネルギー準位の間隔がより小さくなったことで、熱的に励起可能な状態の数が増えたことを表しています。
三次元並進運動の寄与
以上の結果を利用すると、三次元の並進も簡単に考えることができます。
まず、全エネルギーが各方向への一次元並進エネルギーの和となることから、三次元の分配関数は一次元の分配関数の積として書けます。
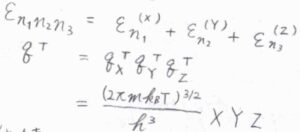
すなわち、\(q^\rm{T}\)\(\displaystyle =\frac{(2\pi mk_\rm{B}\mathit{T})^\frac{3}{2}}{h^3}XYZ\)となります。
ここで\(Y\)と\(Z\)は、それぞれ\(y\)軸方向と\(z\)軸方向についての箱の大きさです。
\(XYZ\)は箱の体積\(V\)で置き換えることができるため、\(q^\rm{T}\)\(\displaystyle =\frac{V}{\Lambda^3}\)と求められます。

この式中の\(\Lambda\)は、先ほど定義した熱波長と同じです。
一次元のときと同様に、分子の質量や温度の増大に伴って、熱波長は小さくなり、並進分配関数は大きくなります。
これを分子論的にイメージすると、こちらの図のようになります。

左が分配関数が小さく、分子数は多い例で、右がその逆です。
分子が三方向へ自由に飛び回るためには、励起可能な状態が多くなくてはいけません。
分子1個あたりの並進状態の数は\(\displaystyle \frac{q^\rm{T}}{N}\)であり、これが十分大きくないと、エネルギーを上限のない連続関数とした近似が使えないと考えます。
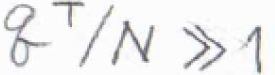
\(q^\rm{T}\)\(\displaystyle =\frac{V}{\Lambda^3}\)を代入すると、\(\displaystyle \frac{q^\rm{T}}{N}=(\frac{d}{\Lambda})^3\)であり、これが十分に大きいというのが条件になります。
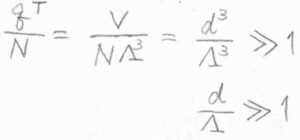
ここで、\(d\)は平均の分子間距離で、\(\displaystyle (\frac{V}{N})^\frac{1}{3}\)です。
したがって、平均の分子間距離に比べて、熱波長が十分小さいときに、この近似はよく成り立つことになります。
例えば、\(25^\circ \rm{C}\)の水素分子では\(71\ \rm{pm}\)であり、\(1\ \rm{mol}\)の気体を入れるための容器の体積が\(210\ \rm{mm}\)\(^3\)よりも十分大きければ、\(q^\rm{T}\)\(\displaystyle =\frac{V}{\Lambda^3}\)と考えることができます。
これよりも質量の大きな気体分子であれば、さらに熱波長は小さいため、実験室で一般的に使う容器では、だいたい近似が成り立つと言えます。
近似が成り立たないときには、有限のエネルギー準位から級数和を計算することになります。
振動分配関数
続いて、振動運動についての分配関数を考えます。
まず、一次元調和振動子のポテンシャルは、\(\displaystyle (v+\frac{1}{2})\hbar\omega\)で与えられます。
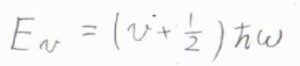
\(v\)は振動量子数で、\(0\)と自然数をとります。
\(\displaystyle \hbar=\frac{h}{2\pi}\)、\(\omega\)は角周波数です。
導出の過程は、こちらを参照してください。

振動分配関数は、等比数列の無限級数の和として、\(\displaystyle \frac{1}{1-\exp{(-\hbar\omega/k_\rm{B}\mathit{T})}}\)と書けます。
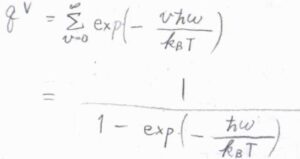
振動特性温度
\(\displaystyle T \gg \frac{\hbar\omega}{k_\rm{B}}\)のときには、指数関数のマクローリン展開の式を利用して、\(q^\rm{V}\)\(\displaystyle \approx \frac{k_\rm{B}\mathit{T}}{\hbar\omega}\)と近似できます。
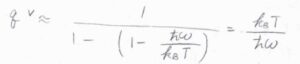
\(\displaystyle \frac{\hbar\omega}{k_\rm{B}}\)のことは、振動特性温度と呼ばれます。
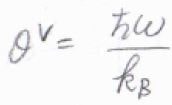
ここでは、\(\theta^\rm{V}\)と表すことにします。
したがって、高温極限では、振動分配関数は絶対温度に比例することになります。
縦軸を振動分配関数、横軸を絶対温度としてグラフを書くと、こちらのようになります。
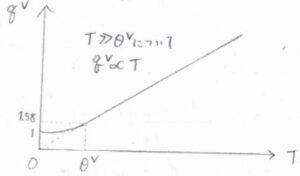
一般的に、振動準位のエネルギー差は、並進や回転よりも大きく、例えば塩化水素では、振動特性温度は\(4304\ \rm{K}\)となります。
分子を構成する原子が軽いほど、振動数は大きくなるため、振動特性温度は高くなります。
低い温度については、分光法などによって得られた振動数から、無限級数の和を計算することで、分配関数を計算できます。
複数の基準振動モードをもつ多原子分子では、それぞれのモードの振動分配関数の積が分子全体の振動分配関数となります。
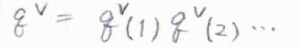
回転分配関数
直線型回転子
始めに、直線型回転子の回転分配関数を考えます。
直線型回転子は\(0\)は、結合軸まわりの慣性モーメントが\(0\)で、それ以外の2つの慣性モーメントが等しくなります。
二原子分子や二酸化炭素が該当します。
その回転準位\(E_J\)は、\(E_J=hc\tilde{B}J(J+1)\)で与えられます。
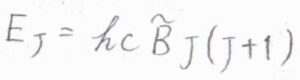
ここで、\(J\)は回転量子数で\(0\)と自然数をとります。
\(c\)は光の速さ、\(\tilde{B}\)は回転定数です。
導出の過程は、こちらの記事を参照してください。

そして、実験室に固定された軸の方向について、量子化されたエネルギーの成分を考えることで、その縮退度は\(2J+1\)とでてきます。
したがって、回転分配関数は\(\displaystyle \sum_{J=0}^\infty (2J+1)\exp{[-\frac{hc\tilde{B}J(J+1)}{k_\rm{B}\mathit{T}}]}\)と書けます。
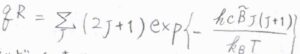
一般的に、回転準位の間隔は、並進よりも大きく、振動よりは小さくなるのですが、ここで回転エネルギーが上限のない連続関数であると考えると、分配関数の近似値を積分によって求めることができます。
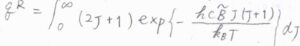
指数である\(\displaystyle \frac{hc\tilde{B}J(J+1)}{k_\rm{B}\mathit{T}}\)を\(x\)とおいて置換積分すると、回転分配関数\(q^\rm{R}\)\(\displaystyle =\frac{k_\rm{B}\mathit{T}}{hc\tilde{B}}\)と計算されます。
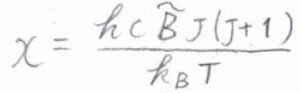
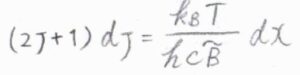
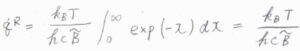
このことより、連続関数の近似が成り立つ温度では、回転分配関数は絶対温度に比例します。
また、回転定数は慣性モーメントに反比例するため、大きい分子や重い分子ほど回転分配関数も大きくなります。
対称回転子
続いて、対称回転子の場合について、考えてみましょう。
対称回転子は、2つの等しい慣性モーメントと、\(0\)ではない3つ目の慣性モーメントをもちます。
具体的には、アンモニアやクロロメタン、ベンゼンなどが該当します。
その回転準位\(E_{J, K}\)は、\(hc\tilde{B}J(J+1)+hc(\tilde{A}-\tilde{B})K^2\)で与えられます。
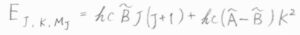
ここで、\(J\)は\(0\)と自然数をとり、\(K\)は\(-J\)から\(J\)までの整数をとります。
\(\tilde{A}\)と\(\tilde{B}\)はいずれも回転定数で、\(\tilde{B}\)の方が2つの等しい慣性モーメントの値からくるものです。
こちらも、縮退度は\(2J+1\)となります。
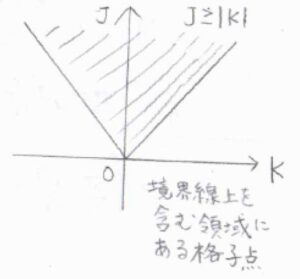
ここで、計算を簡単にするために、\(J\)と\(K\)の条件を違う形で書きます。
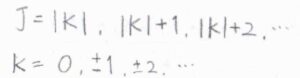
\(K\)はすべての整数をとり、\(J\)は\(|K|\)以上の整数をとるものとします。
横軸を\(K\)、縦軸を\(J\)としたグラフを考えると、先ほどの条件も今の条件も斜線部の領域(境界線上を含む)にある格子点となるので、この2つは同じ意味だとわかります。
このようにして、回転分配関数を変形すると、結局、\(J\)についての級数の和を計算した後、\(K\)に\(-\infty\)から\(\infty\)までの整数を代入して、級数の和を計算すればよいということになります。
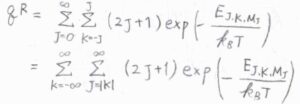
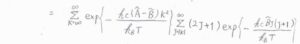
ここで、直線型回転子のときと同様に、エネルギーを連続関数として近似すると、二変数関数の積分として考えることができます。
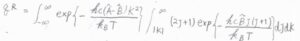
始めに、\(J\)についての積分だけ考えると、その答えは\(\displaystyle \frac{k_\rm{B}\mathit{T}}{hc\tilde{B}}\exp{[-\frac{hc\tilde{B}|K|(|K|+1)}{k_\rm{B}\mathit{T}}]}\)と計算されます。
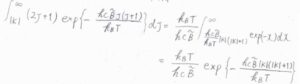
それから、\(|K|(|K|+1)\approx K^2\)と近似して、\(K\)についての積分をすると、ガウス積分の公式より、回転分配関数\(q^\rm{R}\)は、\(\displaystyle (\frac{k_\rm{B}\mathit{T}}{hc})^\frac{3}{2}(\frac{\pi}{\tilde{A}\tilde{B}^2})^\frac{1}{2}\)と計算できます。
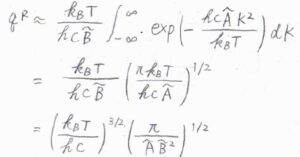
非対称回転子、球対称回転子
この結果を利用すると、非対称回転子や球対称回転子についても、回転分配関数を簡単に求めることができます。
互いに異なる慣性モーメントを3つもつ非対称回転子では、対称回転子の2つの\(\tilde{B}\)のうち、一方を\(\tilde{C}\)と置き換えることで、\(q^\rm{R}\)\(\displaystyle =(\frac{k_\rm{B}\mathit{T}}{hc})^\frac{3}{2}(\frac{\pi}{\tilde{A}\tilde{B}\tilde{C}})^\frac{1}{2}\)となります。
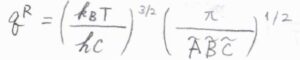
3つの慣性モーメントがすべて同じ値となる球対称回転子では、対称回転子の\(\tilde{A}\)を\(\tilde{B}\)と置き換えて、\(q^\rm{R}\)\(\displaystyle =(\frac{k_\rm{B}\mathit{T}}{hc\tilde{B}})^\frac{3}{2}(\frac{\pi}{\tilde{B}^3})^\frac{1}{2}\)となります。
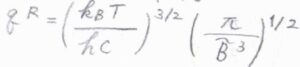
回転特性温度
最後に、ここまでの計算で注意するべきことを2点お話しして、終わります。
まず、回転エネルギーを上限のない連続関数として考えるためには、絶対温度\(T\)が\(\displaystyle \frac{hc\tilde{B}}{k_\rm{B}}\)に比べて、十分に大きくなければいけません。
低い温度については、分光法などによって得られた離散的な回転準位について、級数の和を計算することになります。
\(\displaystyle \frac{hc\tilde{B}}{k_\rm{B}}\)は、回転特性温度と呼ばれており、ここでは\(\theta^\rm{R}\)と表すことにします。
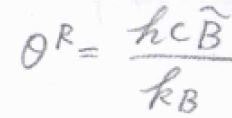
高音域における直線型回転子の回転分配関数は、\(\displaystyle \frac{T}{\theta^\rm{R}}\)になります。
一般的に、軽い原子で構成される分子ほど、回転特性温度は高く、回転近似は成り立ちにくくなります。
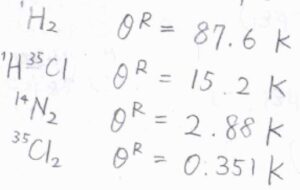
特に、水素分子は\(87.6\ \rm{K}\)と高い回転特性温度をもつため、近似を慎重に行う必要があります。
対称数
そして、注意するべきことの2点目ですが、実は、ここまでの議論では、現実に励起可能な状態の数を過大評価してしまうことがあります。
例えば、対称な二原子分子と非対称な二原子分子を\(\pi\)だけ回転させることを考えてみます。

すると、対称な二原子分子だけ、回転する前の状態と区別できなくなります。
これにより、対称な直線型回転子の励起可能な状態の数は、非対称な直線型回転子のちょうど半分になってしまいます。
すなわち、回転分配関数\(q^\rm{R}\)は、\(\displaystyle \frac{T}{2\theta^\rm{R}}\)となります。
ベンゼンなどより対称性の高い分子であれば、半分よりもさらに分配関数は小さくなるものと考えられます。
そこで、対称数\(\sigma\)を導入して一般化すると、直線型回転子について\(q^\rm{R}\)\(\displaystyle =\frac{T}{\sigma\theta^\rm{R}}\)、直線型以外の任意の回転子について\(q^\rm{R}\)\(\displaystyle =\frac{1}{\sigma}(\frac{k_\rm{B}\mathit{T}}{hc})^\frac{3}{2}(\frac{\pi}{\tilde{A}\tilde{B}\tilde{C}})^\frac{1}{2}\)となります。
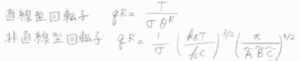
一般的に\(\sigma\)を求めるには、分子の回転部分群、すなわち恒等操作と回転操作だけを考える群の位数を考えます。
点群については、こちらを参照してください。

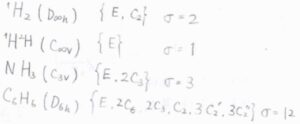
\(D_\rm{\infty h}\)群に属する水素分子では、恒等操作のほかに、二回回転操作が対称操作になるので、対称数は\(2\)となります。
そして、水素原子の一方が重水素に置換されると、\(C_\rm{\infty v}\)群に属することになり、二回回転操作が対称操作ではなくなり、対称数は\(1\)となります。
\(C_\rm{3v}\)群に属するアンモニアでは、恒等操作のほかに、三回回転操作が2つ考えられるので、対称数は\(3\)となります。
\(D_\rm{6h}\)群に属するベンゼンでは、合計で11の回転操作があるので、対称数は\(12\)となります。
量子力学的な起源
対称数で割る操作のより厳密な説明は、特定の状態の占有を禁じるパウリの原理によってなされます。
類似の説明は、回転ラマン分光法についての記事でもしています。

ここでは、対称な直線型回転子である水素分子を例に説明します。
まず、\(\pi\)だけ回転させる操作は、2つの原子のラベルを交換する操作と同じであるとみなせます。
パウリの原理とは、ある2つの同種の粒子のラベルを交換したときに、その粒子が半整数のスピンをもつフェルミ粒子であれば、全波動関数の符号が変化し、整数のスピンをもつボース粒子であれば、全波動関数の符号は変化しないというものです。
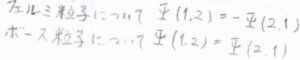
水素の原子核は、\(\displaystyle \frac{1}{2}\)のスピン角運動量をもつフェルミ粒子であるため、\(\pi\)だけ回転したときに全波動関数の符号が変化しない状態は、とりえないということになります。
全波動関数にはスピンも含まれているので、2つの原子核のスピンの相対的な配向によって、許容される状態の数に差が生じます。
球面調和関数は、回転量子数が奇数のときのみ、符号が変化することも考慮すると、水素分子の回転分配関数は、こちらのように書けます。
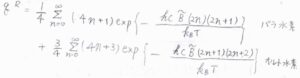
\(J\)が奇数のときには、核スピンが平行なオルト水素のみが許容され、\(J\)が偶数のときには、核スピンが対となるパラ水素のみが許容されます。
それぞれの多重度は\(3\)と\(1\)であることから、奇数の\(J\)については\(\displaystyle \frac{1}{4}\)の状態が禁じられ、偶数の\(J\)については\(\displaystyle \frac{3}{4}\)の状態が禁じられることになります。
横軸に\(J\)、縦軸に各状態の占有数\(N_J\)をとると、こちらの図のようになります。

赤い線は、これは非対称な直線型回転子で予想される占有数の\(1/2\)倍を表したものです。
\(\displaystyle \frac{3}{4}\)と\(\displaystyle \frac{1}{4}\)の平均をとって、励起可能な状態の数は\(\displaystyle \frac{1}{2}\)倍になると近似することができます。
この近似は、より多数の項が寄与する高温域ほど、よく成り立ちます。
また、核スピンの値が\(\displaystyle \frac{1}{2}\)でない原子で構成された分子でも、同じ対称数の値で平均化することができます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!





